题目内容
9.已知直线l过点(1,1)和(0,3),第一象限的点A(a,b)落在直线l上,则$\frac{2a+b}{ab}$的最小值为$\frac{8}{3}$.分析 由已知可得点A(a,b)满足a>0,b>0,2a+b=3,结合基本不等式求出ab的范围,可得$\frac{2a+b}{ab}$的最小值.
解答 解:∵直线l过点(1,1)和(0,3),
故直线l的方程为:x=$\frac{y-3}{1-3}$,即2x+y=3,
由第一象限的点A(a,b)落在直线l上,
可得:a>0,b>0,2a+b=3,
∴2ab≤$\frac{(2a+b)^{2}}{4}$=$\frac{9}{4}$,即ab≤$\frac{9}{8}$
故$\frac{2a+b}{ab}$=$\frac{3}{ab}$≥$\frac{3}{\frac{9}{8}}$=$\frac{8}{3}$,
故答案为:$\frac{8}{3}$
点评 本题考查的知识点是基本不等式,直线方程,是直线与不等式的综合应用,难度中档.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
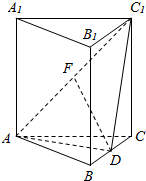 如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,BD=DC,AF=C1F.