题目内容
19．已知偶函数f（x）在[0，+∞）单调递减，若f（x-1）＞f（2），则x的取值范围是（-1，3）．分析 根据函数奇偶性和单调性之间的关系，将不等式进行转化即可．
解答 解：∵偶函数f（x）在[0，+∞）单调递减，
∴不等式f（x-1）＞f（2）等价为f（|x-1|）＞f（2），
则|x-1|＜2，
即-2＜x-1＜2，
则-1＜x＜3，
即不等式的解集为（-1，3），
故答案为：（-1，3）
点评 本题主要考查不等式的求解，利用函数奇偶性和单调性之间的关系进行转化是解决本题的关键．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
10．曲线y=$\frac{1}{3}$x3在点（1，$\frac{1}{3}$）处的切线与直线x+y-3=0的夹角为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
7．
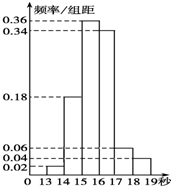某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；…第六组，成绩大于等于18秒且小于等于19秒．如图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班总人数的百分比为x，成绩大于等于15秒且小于17秒的学生人数为y，平均成绩为z，则从频率分布直方图中可分析出x、y、z的值分别为（ ）
某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；…第六组，成绩大于等于18秒且小于等于19秒．如图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班总人数的百分比为x，成绩大于等于15秒且小于17秒的学生人数为y，平均成绩为z，则从频率分布直方图中可分析出x、y、z的值分别为（ ）| A． | 0.9，35，15.86 | B． | 0.9，45，15.5 | C． | 0.1，35，16 | D． | 0.1，45，16.8 |
14．在10个球中有6个红球和4个白球（各不相同），不放回地依次摸出2个球，在第一次摸出红球的条件下，第2次也摸到红球的概率为（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{1}{10}$ | D． | $\frac{5}{9}$ |
7．已知随机变量 ξ 的分布列为P（ξ=k）=$\frac{1}{{2}^{k}}$（ k=1，2，…），则 P（2＜x≤4）为（ ）
| A． | $\frac{3}{16}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{16}$ | D． | $\frac{5}{16}$ |
6．已知{an}为等差数列，若a1+a9=$\frac{π}{3}$，则cos（a3+a7）的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |