题目内容
14.在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{5}{9}$ |
分析 事件“第一次摸到红球且第二次也摸到红球”的概率等于事件“第一次摸到红球”的概率乘以事件“在第一次摸出红球的条件下,第二次也摸到红球”的概率.根据这个原理,可以分别求出“第一次摸到红球”的概率和“第一次摸到红球且第二次也摸到红球”的概率,再用公式可以求出要求的概率.
解答 解:先求出“第一次摸到红球”的概率为:P1=$\frac{6}{10}$=$\frac{3}{5}$,
设“在第一次摸出红球的条件下,第二次也摸到红球”的概率是P2
再求“第一次摸到红球且第二次也摸到红球”的概率为P=$\frac{6×5}{10×9}$=$\frac{1}{3}$,
根据条件概率公式,得:P2=$\frac{P}{{P}_{1}}$=$\frac{5}{9}$,
故选:D.
点评 本题考查了概率的计算方法,主要是考查了条件概率与独立事件的理解,属于中档题.看准确事件之间的联系,正确运用公式,是解决本题的关键.

练习册系列答案
相关题目
2.不等式x2-x-2≥0和x2-(2a+1)x+a2+a>0的解集分别为A和B,且A⊆B,则实数a取值范围是( )
| A. | (0,1) | B. | [0,1] | C. | [-1,1] | D. | (-1,1) |
9.为了考察中学生的性别与是否喜欢数学课程之间的关系,在某校中学生中随机抽取了50名学生,得到如下列联表:
你认为性别与是否喜欢数学课程之间有关系的把握有( )
| 喜欢数学 | 不喜欢数学 | 合计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 合计 | 20 | 30 | 50 |
| A. | 0 | B. | 95% | C. | 99% | D. | 100% |
 .
.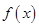 最小正周期;
最小正周期;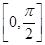 上的最大值和最小值.
上的最大值和最小值. ,则集合
,则集合 ___________.
___________.