题目内容
10.在数列{an}中,(1)已知a1=1,an+1-an=2,求数列{an}的通项公式;
(2)已知a1=1,且nan=(n+1)an-1(n≥2),试求数列{an}的通项公式.
分析 (1)易知数列{an}是以1为首项、2为公差的等差数列,进而计算可得结论;
(2)通过nan=(n+1)an-1(n≥2)可知$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+1}{n}$、$\frac{{a}_{n-1}}{{a}_{n-2}}$=$\frac{n}{n-1}$、…、$\frac{{a}_{3}}{{a}_{2}}$=$\frac{4}{3}$、$\frac{{a}_{2}}{{a}_{1}}$=$\frac{3}{2}$,累乘计算即得结论.
解答 解:(1)∵a1=1,an+1-an=2,
∴数列{an}是以1为首项、2为公差的等差数列,
∴an=1+2(n-1)=2n-1;
(2)∵nan=(n+1)an-1(n≥2),
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+1}{n}$(n≥2),
∴$\frac{{a}_{n-1}}{{a}_{n-2}}$=$\frac{n}{n-1}$,
…
$\frac{{a}_{3}}{{a}_{2}}$=$\frac{4}{3}$,
$\frac{{a}_{2}}{{a}_{1}}$=$\frac{3}{2}$,
∴$\frac{{a}_{n}}{{a}_{1}}$=$\frac{3•4•…•n•(n+1)}{2•3•…•(n-1)•n}$=$\frac{n+1}{2}$,
又∵a1=1,
∴an=$\frac{n+1}{2}$•a1=$\frac{n+1}{2}$,
又∵当n=1时满足上式,
∴an=$\frac{n+1}{2}$.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
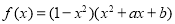 的图象关于直线
的图象关于直线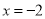 对称,则
对称,则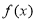 的最大值为 .
的最大值为 .