题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AB=BC=2,∠ABC=120°,AD=CD= ![]() ,直线PC与平面ABCD所成角的正切为
,直线PC与平面ABCD所成角的正切为 ![]() .
. 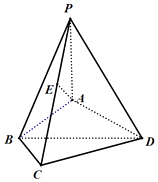
(1)设E为直线PC上任意一点,求证:AE⊥BD;
(2)求二面角B﹣PC﹣A的正弦值.
【答案】
(1)解:设O为线段AC的中点,由AB=BC知BO⊥AC,由AD=CD知DO⊥AC,从而B,O,D三点共线,即O为AC与DB的交点
又PA⊥平面ABCD,所以PA⊥BD
又AC∩PA=A,所以DB⊥平面PAC
因为E为直线PC上任意一点,所以AE平面PAC,所以AE⊥BD
(2)解:以 ![]() 所在方向为x轴,
所在方向为x轴, ![]() 所在方向为y轴,过O作AP的平行线为z轴,建立空间直角坐标系
所在方向为y轴,过O作AP的平行线为z轴,建立空间直角坐标系
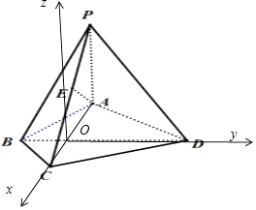
由题意,AC=2 ![]() ,OB=1,OD=2
,OB=1,OD=2
又PA⊥平面ABCD,故直线PC与平面ABCD所成角即为∠PCA,∴tan∠PCA ![]()
所以PA= ![]() ,所以B(﹣1,0,0),C(0,﹣
,所以B(﹣1,0,0),C(0,﹣ ![]() ,0),P(0,
,0),P(0, ![]() ,
, ![]() )
)
![]() ,
, ![]() ∴
∴
设平面BPC的法向量 ![]() ,由
,由 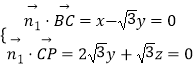 ,有
,有
解得 ![]() …(10分)
…(10分)
由(1),取平面PCA的法向量 ![]() .
.
所以cos< ![]() >=
>= ![]()
所以二面角B﹣PC﹣A的正弦值为 ![]()
【解析】(1)设O为线段AC的中点,由AB=BC知BO⊥AC,由AD=CD知DO⊥AC,从而B,O,D三点共线,即O为AC与DB的交点,可得DB⊥平面PAC即可得AE⊥BD;(2)以 ![]() 所在方向为x轴,
所在方向为x轴, ![]() 所在方向为y轴,过O作AP的平行线为z轴,建立空间直角坐标系由题意,AC=2
所在方向为y轴,过O作AP的平行线为z轴,建立空间直角坐标系由题意,AC=2 ![]() ,OB=1,OD=2,又PA⊥平面ABCD,故直线PC与平面ABCD所成角即为∠PCA,由tan∠PCA
,OB=1,OD=2,又PA⊥平面ABCD,故直线PC与平面ABCD所成角即为∠PCA,由tan∠PCA ![]() 求得PA,利用向量求解
求得PA,利用向量求解
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能正确解答此题.

 金博士一点全通系列答案
金博士一点全通系列答案【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为
精确到0.1),若某天的气温为![]() ,预测这天热奶茶的销售杯数;
,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取两天,求所选取两天中至少有一天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.
