题目内容
(本题满分10分)已知数列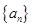 的首项
的首项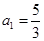 ,
,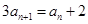 ,
,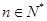 ,
,
(1)求证:数列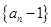 为等比数列;
为等比数列;
(2)若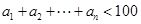 ,求最大的正整数
,求最大的正整数 .
.
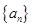 的首项
的首项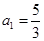 ,
,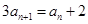 ,
,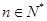 ,
,(1)求证:数列
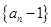 为等比数列;
为等比数列;(2)若
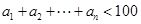 ,求最大的正整数
,求最大的正整数 .
.(1)证明见解析(2)99.
试题分析:(1)本小题关键是把递推关系式
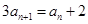 配凑成
配凑成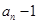 与
与 的关系,再利用等比数列的定义加以说明即可;(2)本小题利用(1)的结论,可写出数列
的关系,再利用等比数列的定义加以说明即可;(2)本小题利用(1)的结论,可写出数列 的通项公式,由此可求出其前n项和,再利用已知条件的不等式可找到最大的正整数
的通项公式,由此可求出其前n项和,再利用已知条件的不等式可找到最大的正整数 .
.试题解析:(1)∵
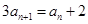 ,∴
,∴ ,且
,且 ,∴数列
,∴数列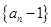 是以
是以 为首项,
为首项,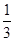 为公比的等比数列.
为公比的等比数列.(2)由(1)可求得
 ,∴
,∴ ,又
,又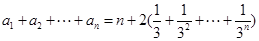
 ,若
,若 ,则
,则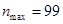 .
.
练习册系列答案
相关题目
 为等比数列,
为等比数列,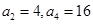 ,记
,记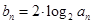 .
.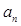 和
和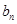 ;
;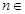
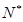 ,有
,有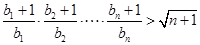 成立.
成立.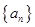 中,
中,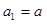 ,
,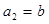 ,
,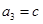 ,
,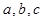 分别为△ABC的三个内角A,B,C的对边,且
分别为△ABC的三个内角A,B,C的对边,且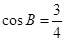 .
.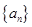 的公比
的公比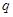 ;
;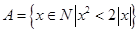 ,且
,且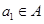 ,求数列
,求数列 满足
满足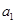 =1,
=1, .
. 是等比数列,并求
是等比数列,并求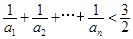 .
.