题目内容
等差数列{an}中,已知a1=
,a2+a5=4,an=33,则n的值为( )
| 1 |
| 3 |
| A.50 | B.49 | C.48 | D.47 |
设公差为d,
∵a1=
,a2+a5=4,∴a1+d+a1+4d=4,即
+5d=4,可得d=
.
再由an=a1+(n-1)d=
+(n-1)×
=33,解得 n=50,
故选 A.
∵a1=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
再由an=a1+(n-1)d=
| 1 |
| 3 |
| 2 |
| 3 |
故选 A.

练习册系列答案
相关题目
 的首项
的首项 ,
, ,
, ,
, 为等比数列;
为等比数列; ,求最大的正整数
,求最大的正整数 .
. 的前
的前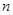 项和为
项和为 ,已知
,已知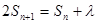 (
( ,
,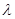 为常数),
为常数),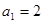 ,
, ,(1)求数列
,(1)求数列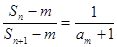 成立的正整数
成立的正整数 ,
,