题目内容
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(1)求an,bn; (2)求数列{an·bn}的前n项和Tn.
(1)求an,bn; (2)求数列{an·bn}的前n项和Tn.
(1)an=4n-1,bn=2n-1(n∈N*);(2)Tn=5+(4n-5)×2n.
试题分析:(1)本小题中已知Sn是数列{an}的前n项和,且Sn的表达式已知,当n≥2时,an=Sn-Sn-1,而当n=1时,a1=S1且检查是否符合前式,在an求出之后利用an=4log2bn+3求得bn;(2)可知an·bn的表达式是等差乘以等比形式,求这类数列的前n项和Tn,只需用错位相减法可完成求和,即若等比数列的公比为q,则由Tn -qTn进行错位相减,整理出Tn即可.
试题解析:(1)由Sn=2n2+n,可得:当n≥2时,an=Sn-Sn-1=(2n2+n)-[2(n-1)2+(n-1)]="4n-1," 当n=1时,a1=3符合上式,所以an=4n-1(n∈N*).由an=4log2bn+3,可得4n-1=4log2bn+3, 解得bn=2n-1(n∈N*).
(2)anbn=(4n-1)·2n-1, ∴Tn=3+7×21+11×22+15×23+…+(4n-1)×2n-1, ①
2Tn=3×21+7×22+11×23+15×24+…+(4n-1)×2n, ②
①-②可得:
-Tn=3+4[21+22+23+24+…+2n-1]-(4n-1)×2n=3+4×
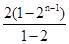 -(4n-1)×2n=-5+(5-4n)×2n,
-(4n-1)×2n=-5+(5-4n)×2n, ∴Tn=5+(4n-5)×2n.
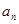 与
与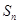 的关系:
的关系: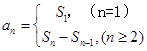 ,错位相减法求和.
,错位相减法求和.
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
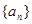 是公比为
是公比为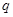 的等比数列,推导
的等比数列,推导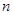 项公式.
项公式.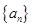 的首项
的首项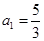 ,
,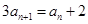 ,
,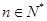 ,
,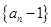 为等比数列;
为等比数列;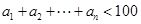 ,求最大的正整数
,求最大的正整数 .
.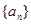 中,
中,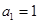 ,
,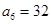 ,
, 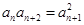 (
(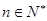 ),把数列的各项按如下方法进行分组:(
),把数列的各项按如下方法进行分组:(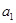 )、(
)、(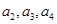 )、(
)、(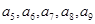 )、 ,记
)、 ,记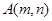 为第
为第 组的第
组的第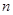 个数(从前到后),若
个数(从前到后),若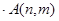 =
=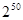 ,则
,则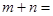 _________.
_________.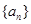 的公比为
的公比为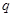 ,前
,前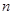 项和
项和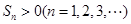 ,求
,求