Question

【题目】已知圆 的圆心为原点 ，且与直线 相切。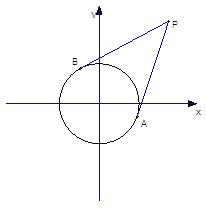
（1）求圆 的方程；
（2）过点 (8,6)引圆O的两条切线 ，切点为 ，求直线 的方程.

Answer 1

【答案】
（1）依题意得：圆 的半径 ，

所以圆 的方程为 。

（2） 是圆 的两条切线， 。 在以 为直径的圆上。点 的坐标为 ，则线段 的中点坐标为 。

以 为直径的圆方程为

化简得： , 为两圆的公共弦，

直线 的方程为 即 。

【解析】分析：本题主要考查了圆的切线方程、直线与圆的位置关系、相交弦所在直线的方程，解决问题的关键是(1)根据弦心距关系求得半径即可解决问题；(2)根据 是圆 的两条切线，得到 ，所以 在以 为直径的圆上，根据所给条件可得一 为直径的圆方程为 ,联立两圆方程可得公共弦所在直线方程，