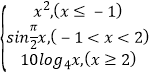题目内容
【题目】已知函数f（x）+2= 
，当x∈（0，1]时，f（x）=x2 ， 若在区间（﹣1，1]内，g（x）=f（x）﹣t（x+2）有两个不同的零点，则实数t的取值范围是（ ）
A.（0， 
]
B.（0， 
]
C.[﹣ ， ]
D.[﹣ ， ]
【答案】A
【解析】解：由题意得：
当x=0时，f（0）+2= 
=2，所以f（0）=0，
当x∈（﹣1，0]，即 
∈（0，1]时，
f（ ）=（ ）2=x+1，
所以f（x）+2= 
= 
，
所以f（x）= ﹣2，
故函数f（x）的图象如下图所示：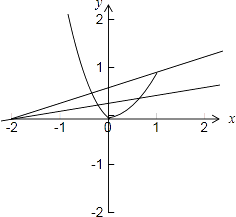
若g（x）=f（x）﹣t（x+2）有两个不同的零点，
则函数f（x）的图象与y=t（x+2）的图象有两个交点，
故t∈（0， 
]，
故选：A
练习册系列答案
阅读快车系列答案
相关题目
