题目内容
【题目】在三棱柱![]() 中,已知侧棱
中,已知侧棱![]() 底面
底面![]() 为
为![]() 的中点,
的中点, ![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找,往往从两个方面出发,一是利用线面垂直性质定理得线线垂直,二是利用平几知识,结合勾股定理得线线垂直,(2)求点到直线距离,往往利用等体积法求高得到.
试题解析:
解:(1) 证明:在![]() 中,
中, ![]() 为
为![]() 的中点,故
的中点,故![]() ,又侧棱
,又侧棱![]() 底面
底面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,则
,则![]() ,在
,在![]() 中,
中,
![]() ;在
;在![]() 中,
中, ![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
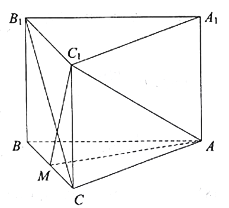
(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由于
,由于![]() ,即
,即![]() ,于是
,于是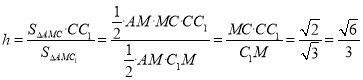 ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
点睛:利用等积法可以用来求解几何图形的高或几何体的高或内切球的半径,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.

练习册系列答案
相关题目