Question

【题目】已知圆心在 轴上的圆 过点 和 ，圆 的方程为 ．
（1）求圆 的方程；
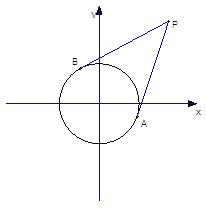
（2）由圆 上的动点 向圆 作两条切线分别交 轴于 ， 两点，求 的取值范围．

Answer 1

【答案】
（1）设 ， ，

依题意得，圆 的圆心为线段 的垂直平分线 与 轴的交点 ．

因为直线 的方程为 ，即 ，

所以圆心 的坐标为 ．

所以圆 的方程为 ．

（2）设圆 上的动点 的坐标为 ，

则 ，

即 ，

解得 ．

设点 ， ，

则直线 ： ，即 ，

因为直线 与圆 相切，所以 ，

化简得 ． ①

同理得 ， ②

由①②知 ， 为方程 的两根，

即

所以

．

因为 ，

所以

．

令 ，因为 ，所以 ．

所以 ，

当 时， ，

当 时， ．

所以 的取值范围为 ．

【解析】分析：本题主要考查了圆方程的综合应用，解决问题的关键是（1）先设圆的标准方程，再利用已知条件可得 和 的值，即可得圆 的方程；（2）先设圆 上的动点 的坐标为 ，则可得 的取值范围，再写出 ， 的方程，可得 和 的坐标，进而可得 ，利用函数的单调性，可得 的最大值和最小值，即可得 的取值范围．