题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若不等式
时,若不等式![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】
(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)当
的减区间;(2)当![]() 时,不等式
时,不等式![]() 在
在![]() 时恒成立,等价于
时恒成立,等价于![]() 在(1,+∞)上恒成立,令
在(1,+∞)上恒成立,令![]() ,先证明当
,先证明当![]() 时,不合题意,再分两种情况讨论即可筛选出符合题意的实数
时,不合题意,再分两种情况讨论即可筛选出符合题意的实数![]() 的取值范围.
的取值范围.
(1)由题意,知![]() ,
,
∵当a<0,x>0时,有![]() .
.
∴x>1时,![]() ;当0<x<1时,
;当0<x<1时,![]() .
.
∴函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
(2)由题意,当a=1时,不等式![]() 在x∈(1,+∞)时恒成立.
在x∈(1,+∞)时恒成立.
整理,得![]() 在(1,+∞)上恒成立.
在(1,+∞)上恒成立.
令![]() .
.
易知,当b≤0时,![]() ,不合题意.
,不合题意.
∴b>0
又![]() ,
,![]() .
.
①当b≥![]() 时,
时,![]() .又
.又![]() 在[1,+∞)上单调递减.
在[1,+∞)上单调递减.
∴![]() 在[1,+∞)上恒成立,则h(x)在[1,+∞)上单调递减.
在[1,+∞)上恒成立,则h(x)在[1,+∞)上单调递减.
所以![]() ,符合题意;
,符合题意;
②![]() 时,
时,![]() ,
,![]() ,
,
又![]() 在[1,+∞)上单调递减,
在[1,+∞)上单调递减,
∴存在唯一x0∈(1,+∞),使得![]() .
.
∴当h(x)在(1,x0)上单调递增,在(x0,+∞)上单调递减.
又h(x)在x=1处连续,h(1)=0,∴h(x)>0在(1,x0)上恒成立,不合题意.
综上所述,实数b的取值范围为[![]() ,+∞ ).
,+∞ ).

【题目】如图,“六芒星”是由两个全等正三角形组成,中心重合于点![]() 且三组对边分别平行,点
且三组对边分别平行,点![]() 是“六芒星”(如图)的两个顶点,动点
是“六芒星”(如图)的两个顶点,动点![]() 在“六芒星”上(内部以及边界),若
在“六芒星”上(内部以及边界),若![]() ,则
,则![]() 的取值可能是( )
的取值可能是( )
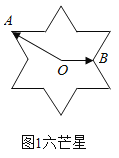
A.![]() B.1C.5D.9
B.1C.5D.9
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: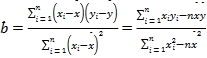 ,
,![]() .
.