题目内容
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2) ![]()
【解析】
(1)由余弦定理得能求出AD的长.
(2)由正弦定理得![]() ,从而BC=3
,从而BC=3![]() ,DC
,DC![]() ,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,则可求AE
,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,则可求AE![]() ,CF
,CF![]() ,四边形ABCD的面积:S=S△ABD+S△BDC
,四边形ABCD的面积:S=S△ABD+S△BDC![]() ,由此能求出结果.
,由此能求出结果.
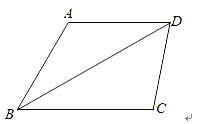
(1)∵在四边形ABCD中,AD∥BC,AB![]() ,∠A=120°,BD=3.
,∠A=120°,BD=3.
∴由余弦定理得:cos120°![]() ,
,
解得AD![]() (舍去AD=﹣2
(舍去AD=﹣2![]() ),
),
∴AD的长为![]() .
.
(2)∵AD∥BC,AB![]() ,∠A=120°,BD=3,AD
,∠A=120°,BD=3,AD![]() ,
,
∠BCD=105°,
∴∠DBC=30°,∠BDC=45°,
∴![]() ,
,
解得BC=3![]() ,DC
,DC![]() ,
,
如图,过A作AE⊥BD,交BD于E,过C作CF⊥BD,交BD于F,
则AE![]() ,CF
,CF![]() ,
,
∴四边形ABCD的面积:
S=S△ABD+S△BDC![]()
![]()
![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目