题目内容
【题目】已知直线PA,PB分别与半径为1的圆O相切于点A,B,PO=2, ![]() .若点M在圆O的内部(不包括边界),则实数λ的取值范围是( )
.若点M在圆O的内部(不包括边界),则实数λ的取值范围是( )
A.(﹣1,1)
B.![]()
C.![]()
D.(0,1)
【答案】B
【解析】解法一:如图,在线段PA的延长线上取点Q,使得PA=AQ,连接OQ,交圆于C, 由圆的半径为1,PO=2可得∠BOP=∠AOP=∠AOQ=60°,PB= ![]() ,故B,O,Q三点共线,且BQ=3
,故B,O,Q三点共线,且BQ=3
因为2 ![]() =
= ![]() ,∴
,∴ ![]() =λ
=λ ![]() +(1﹣λ)
+(1﹣λ) ![]() .
. ![]() .
.
由点M在圆O的内部(不包括边界),∴0< ![]()
故选:B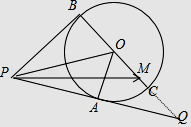
解法二:以O为原点, ![]() 的方向为x轴正方向建立平面直角坐标系,则P(2,0)
的方向为x轴正方向建立平面直角坐标系,则P(2,0)
A( ![]() ),B(
),B( ![]() ,﹣
,﹣ ![]() ),设M(x0 , y0),
),设M(x0 , y0),
由 ![]() .得
.得 ![]() ,y0=
,y0= ![]() ,
,
∵M(x0 , y0)在圆O的内部(不包括边界),∴ ![]() ,
,
整理得﹣1<3λ﹣1<1,解得0< ![]()
故选:B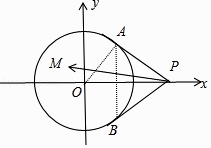
【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点,需要掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

