题目内容
【题目】已知函数![]() .
.
⑴若函数![]() 的图象经过点
的图象经过点![]() ,求实数
,求实数![]() 的值.
的值.
⑵当![]() 时,函数
时,函数![]() 的最小值为1,求当
的最小值为1,求当![]() 时,函数
时,函数![]() 最大值.
最大值.
【答案】⑴b=2;⑵见解析.
【解析】
(1)把点的坐标代入f(x)计算;
(2)对f(x)的对称轴与区间[﹣1,2]的关系进行分情况讨论,判断f(x)的单调性,利用单调性解出b,再求出最大值.
解:(1)把(4,3)代入f(x)得16﹣8b+3=3,∴b=2.
(2)f(x)的图象开口向上,对称轴为x=b.
①若b≤﹣1,则f(x)在[﹣1,2]上是增函数,
∴fmin(x)=f(﹣1)=4+2b=1,解得b=﹣![]() .
.
∴fmax(x)=f(2)=7﹣4b=13.
②若b≥2,则f(x)在[﹣1,2]上是减函数,
∴fmin(x)=f(2)=7﹣4b=1,解得b=![]() (舍).
(舍).
③若﹣1<b<2,则f(x)在[﹣1,b]上是减函数,在(b,2]上增函数.
∴fmin(x)=f(b)=﹣b2+3=1,解得b=![]() 或b=﹣
或b=﹣![]() (舍).
(舍).
∴fmax(x)=f(﹣1)=4+2b=4+2![]() .
.
综上,当b≤﹣1时,f(x)的最大值为13,当﹣1<b<2时,f(x)最大值为4+2![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了了解某省各景区在大众中的熟知度,随机从本省![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家![]() 级旅游景区?”,统计结果如下表所示:
级旅游景区?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
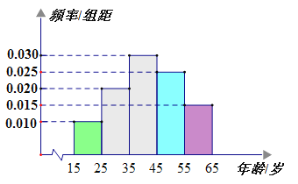
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄段在
人,求所抽取的人中恰好没有年龄段在![]() 的概率
的概率
【题目】![]() 年
年![]() 月
月![]() 日是第二十七届“世界水日”,
日是第二十七届“世界水日”,![]() 月
月![]() 日是第三十二届“中国水周”.我国纪念
日是第三十二届“中国水周”.我国纪念![]() 年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取
年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取![]() 、
、![]() 两个小区各
两个小区各![]() 户家庭,记录他们
户家庭,记录他们![]() 月份的用水量(单位:
月份的用水量(单位:![]() )如下表:
)如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据两组数据完成下面的茎叶图,从茎叶图看,哪个小区居民节水意识更好?
|
| |
| ||
| ||
| ||
|
(2)从用水量不少于![]() 的家庭中,
的家庭中,![]() 、
、![]() 两个小区各随机抽取一户,求
两个小区各随机抽取一户,求![]() 小区家庭的用水量低于
小区家庭的用水量低于![]() 小区的概率.
小区的概率.

