Question

【题目】在平面直角坐标系xOy中，抛物线C：x2=2py（p＞0）的焦点为F，过F的直线l交C于A，B两点，交x轴于点D，B到x轴的距离比|BF|小1．
（Ⅰ）求C的方程；
（Ⅱ）若S△BOF=S△AOD ， 求l的方程．

Answer 1

【答案】解：（Ⅰ）解法一：抛物线C：x2=2py（p＞0）的焦点为F（0， ），C的准线方程为 ， 由抛物线的定义，可知|BF|等于点B到C的准线的距离．
又因为点B到x轴的距离比|BF|小1，
所以点B到x轴的距离比点B到抛物线准线的距离小1，
故 ，解得p=2，
所以C的方程为x2=4y．
解法二：C的焦点为 ，
将 代入x2=2py，得x=p或x=﹣p，故 ，
因为点B到x轴的距离比|BF|小1， ，即 ，
解得p=2，所以C的方程为x2=4y，
经检验，抛物线的方程x2=4y满足题意．
（Ⅱ）由（Ⅰ）得C的焦点为F（0，1），设直线l的方程为y=kx+1（k≠0），A（x1 ， y1），B（x2 ， y2）．则 ．
联立方程组 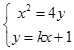消去y，得x2﹣4kx﹣4=0．
△=（﹣4k）2﹣4×1×（﹣4）=16k2+16＞0，
由韦达定理，得x1+x2=4k，x1x2=﹣4．
设点O到直线l的距离为d，则 ， ．
又S△BOF=S△AOD ， 所以|BF|=|AD|．
又A，B，D，F在同一直线上，所以 ，即 ，
因为 ，
所以 ，整理，得16k4+16k2﹣1=0，
故 ，解得 ，
所以l的方程为
【解析】（Ⅰ）解法一：由抛物线的焦半径公式，点B到x轴的距离比点B到抛物线准线的距离小1， ，即可求得p的值，求得抛物线方程； 解法二：将 代入x2=2py，得x=p或x=﹣p，故 ，由点B到x轴的距离比|BF|小1， ，即 ，即可求得p的值，求得抛物线方程；（Ⅱ）设直线l的方程，代入抛物线方程，由S△BOF=S△AOD ， 则|BF|=|AD|．利用韦达定理可得： ，即 ，则两边平方，即可求得k的值，求得直线l的方程．