题目内容
8.已知直线x+y-a=0与圆x2+y2=2交于A、B两点,O是坐标原点,向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足条件|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|,则实数a的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | ±1 |
分析 根据|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|,可知∠AOB=90°,故原点O到直线的x+y-a=0的距离为1,可求得a的值.
解答 解:由|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|,两边平方,得$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
所以∠AOB=90°,则△AOB为等腰直角三角形,
而圆x2+y2=2的半径AO=$\sqrt{2}$,则原点O到直线的x+y-a=0的距离为1,
所以$\frac{|0+0-a|}{\sqrt{1+1}}$=1,即a的值为$\sqrt{2}$或-$\sqrt{2}$.
故选:C.
点评 本题考查了直线与圆相交的性质,熟练正确运用已知条件以及点到直线的距离是解决此问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
16.集合A={0,2},B={1,a2},若A∪B={0,1,2,4},则实数a的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
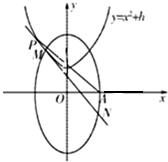 已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.
已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.