题目内容
13.函数$f(x)=4cos(\frac{x}{2}+\frac{π}{3})$(x∈R)的最小正周期为4π.分析 由条件利用y=Asin(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,求得结果.
解答 解:函数$f(x)=4cos(\frac{x}{2}+\frac{π}{3})$(x∈R)的最小正周期为$\frac{2π}{\frac{1}{2}}$=4π,
故答案为:4π.
点评 本题主要考查三角函数的周期性及其求法,利用了y=Asin(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,属于基础题.

练习册系列答案
相关题目
4.如图是一个算法的流程图,则输出S的值是( )
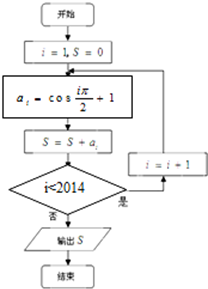

| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
8.已知直线x+y-a=0与圆x2+y2=2交于A、B两点,O是坐标原点,向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足条件|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|,则实数a的值为( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | ±1 |
18.下列函数中,在其定义域内既是偶函数又在(-∞,0)上单调递增的函数是( )
| A. | f(x)=x2 | B. | f(x)=-log2|x| | C. | f(x)=3|x| | D. | f(x)=sinx |