题目内容
17．P是正六边形ABCDEF某一边上一点，$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AF}$，则x+y的最大值为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 设六边形边长为2，把向量$\overrightarrow{AB}$和向量$\overrightarrow{AF}$，沿着AD方向和垂直于AD两个方向分解．设AD方向为x轴，垂直于AD方向为y轴距离坐标系，得到$\overrightarrow{AP}$的坐标，分析x+y去最大值是P的位置．
解答 解：设六边形边长为2，把向量$\overrightarrow{AB}$和向量$\overrightarrow{AF}$，沿着AD方向和垂直于AD两个方向分解．
设AD方向为x轴，垂直于AD方向为y轴如图：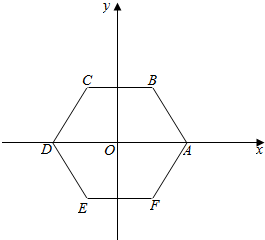
那么$\overrightarrow{AB}$=$\overrightarrow{OC}$=（-1，$\sqrt{3}$），$\overrightarrow{AF}=\overrightarrow{OE}$=（-1，-$\sqrt{3}$）
$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AF}$=（-x-y，$\sqrt{3}$（x-y））
所以，当$\overrightarrow{AP}$的横坐标最小的时候，x+y最大．
那么，当P与D重合时，满足这一条件．
此时AP=4，x+y=4
最大值为4；
故选A．
点评 本题考查了平面向量的坐标运算；关键是适当建立坐标系，得到向量的坐标．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．已知直线x+y-a=0与圆x2+y2=2交于A、B两点，O是坐标原点，向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足条件|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|，则实数a的值为（ ）
| A． | $\sqrt{2}$ | B． | -$\sqrt{2}$ | C． | ±$\sqrt{2}$ | D． | ±1 |
1．某中学为了研究学生的视力和座位（有关和无关）的关系，运用2×2列联表进行独立性研究，经计算K2=7.069，则至少有（ ）的把握认为“学生的视力与座位有关”．
附：
附：
| P（K2≥k0） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A． | 95% | B． | 99% | C． | 97.5% | D． | 90% |