题目内容
12.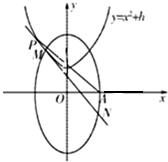 已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.
已知焦点在y轴上的椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)经过点Q($\frac{\sqrt{3}}{2}$,1),过椭圆的一个焦点且垂直长轴的弦长为1.(1)求椭圆C1的方程;
(2)过抛物线C2:y=x2+h(h∈R)上一点P的切线与椭圆C1交于不同两点M,N.点A为椭圆C1的右顶点,记线段MN与PA的中点分别为G,H点,当直线CH与x轴垂直时,求h的最小值.
分析 (1)通过将点Q($\frac{\sqrt{3}}{2}$,1)、y=c代入椭圆方程,计算即得结论;
(2)通过设P(t,t2+h),则直线MN的方程为:y=2tx-t2+h,代入椭圆方程,利用中点坐标公式及韦达定理计算即得结论.
解答 解:(1)∵椭圆过点Q($\frac{\sqrt{3}}{2}$,1),∴$\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1$,
将y=c代入椭圆方程得:x=±$\frac{{b}^{2}}{a}$,∴$\frac{2{b}^{2}}{a}$=1,
解得:a=2,b=1,
∴椭圆C1的方程为:${x}^{2}+\frac{{y}^{2}}{4}=1$;
(2)设P(t,t2+h),由y′=2x可知切线斜率k=2t,
∴直线MN的方程为:y=2tx-t2+h,
将其代入椭圆方程得:4x2+(2tx-t2+h)2-4=0,
化简得:4(1+t2)x2-4t(t2-h)x+(t2-h)2-4=0,
∵直线MN与椭圆交于不同的两点,∴△>0,
即△=16[-t4+2(h+2)t2-h2+4]>0 (*)
设M(x1,y1),N(x2,y2),线段MN中点横坐标为x0,
由韦达定理可知:x1+x2=$\frac{t({t}^{2}-h)}{1+{t}^{2}}$,x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{t({t}^{2}-h)}{2(1+{t}^{2})}$,
设线段PA中点的横坐标为x3,则x3=$\frac{1+t}{2}$,
由已知有x0=x3,即$\frac{t({t}^{2}-h)}{2(1+{t}^{2})}$=$\frac{1+t}{2}$,
显然t≠0,h=-(t+$\frac{1}{t}$+1),
当t>0时,t+$\frac{1}{t}$≥2,当且仅当t=1时取等号,
此时h≤-3,不符合(*)式,舍去;
当t<0时,(-t)+$\frac{1}{-t}$≥2,当且仅当t=-1时取等号,
此时h≥1,符合(*)式;
综上所述,h的最小值为1.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | ±1 |
附:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 95% | B. | 99% | C. | 97.5% | D. | 90% |
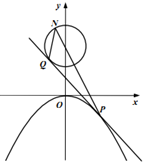 如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.
如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.