已知函数f(x)=$\frac{1}{{4}^{x}+1}$+a是奇函数.则实数a=$-\frac{1}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

3．已知函数f（x）=$\frac{1}{{4}^{x}+1}$+a是奇函数，则实数a=$-\frac{1}{2}$．

分析利用已知函数为奇函数，并且定义域为R，所以f（0）=0，得到关于a的方程解之．

解答解：因为已知函数的定义域为R，并且是奇函数，所以f（0）=0，即$\frac{1}{{4}^{0}+1}+a=0$，即$\frac{1}{2}$+a=0，解得a=-$\frac{1}{2}$；
故答案为：$-\frac{1}{2}$．

点评本题考查了奇函数性质的运用；如果奇函数在x=0处有意义，那么f（0）=0．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

14．若x（xlnx）′=lnx+1，a=${∫}_{1}^{e}$lnxd_x，a¹⁰⁰+2C${\;}_{100}^{1}$a⁹⁹+2²C${\;}_{100}^{2}$a⁹⁸+…+2⁹⁹C${\;}_{100}^{1}$a+2¹⁰⁰被10除得的余数为（　　）

11．三个正数成等比数列，它们的和等于21，倒数的和等于$\frac{7}{12}$，求这三个数．

18．若向量$\overrightarrow{a}$=（2，x+1），$\overrightarrow{b}$=（x+2，6），又$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为锐角，则实数x的取值范围为（　　）

A．

{x|x＞-$\frac{5}{4}$且x≠2}

B．

{x|x＞-$\frac{5}{4}$}

C．

{x|x＜-$\frac{5}{4}$且x≠-5}

D．

{x|x＜-$\frac{5}{4}$}

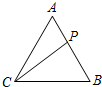8．已知直线x+y-a=0与圆x²+y²=2交于A、B两点，O是坐标原点，向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足条件|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\overrightarrow{OA}$-$\overrightarrow{OB}$|，则实数a的值为（　　）

15．

如图，在等边三角形ABC中，P在线段AB上，且$\overrightarrow{AP}=λ\overrightarrow{AB}$，其中0＜λ＜1，若$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{AB}$=0，则λ的值为$\frac{{2-\sqrt{2}}}{2}$．

12．已知集合A={x|y=$\sqrt{1-{x}^{2}}$，x∈z}，B={p-q|p∈A，q∈A}，则B中元素个数为（　　）

7．曲线C上任意一点p与两点（-2，0），（2，0）连线的斜率的乘积为-$\frac{1}{2}$．
（1）求曲线C 的轨迹方程；
（2）过点M（1，1）的直线l与曲线C交于A、B两点，且M点是线段AB的中点，求直线l的方程并求线段AB的长．

试题分类