题目内容
(本题满分14分) 已知函数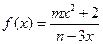 是定义域上的奇函数,且
是定义域上的奇函数,且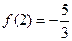 ;函数
;函数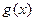 是
是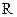 上的增函数,
上的增函数,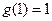 且对任意
且对任意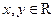 ,总有
,总有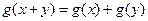
(Ⅰ)函数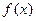 的解析式;
的解析式;
(Ⅱ)判断函数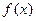 在
在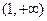 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅲ)若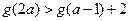 ,求实数
,求实数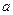 的取值范围.
的取值范围.
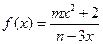 是定义域上的奇函数,且
是定义域上的奇函数,且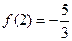 ;函数
;函数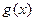 是
是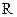 上的增函数,
上的增函数,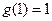 且对任意
且对任意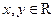 ,总有
,总有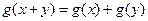
(Ⅰ)函数
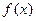 的解析式;
的解析式;(Ⅱ)判断函数
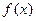 在
在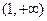 上的单调性,并加以证明;
上的单调性,并加以证明;(Ⅲ)若
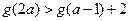 ,求实数
,求实数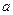 的取值范围.
的取值范围.(1)

(2)略
(3)
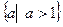
解(Ⅰ)∵
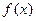 是奇函数,
是奇函数,∴对定义域内的任意的
 ,都有
,都有 ,
,即

整理得:
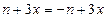
∴

又∵
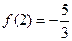
∴
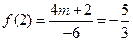 ,解得
,解得
∴所求解析式为
 …………………………………4分
…………………………………4分(Ⅱ)由Ⅰ)可得

任取
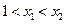 ,
,则由于

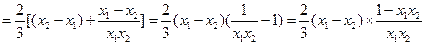

∴

令
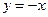 得
得 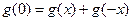
∴
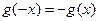
又函数的定义域为
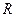
∴
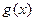 为奇函数
为奇函数∵
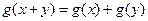 又
又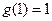
∴
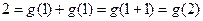
∴
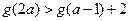 即为
即为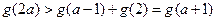
∴
 又函数
又函数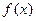 是
是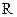 上的增函数
上的增函数 ∴
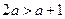 得
得
∴
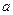 的取值范围是
的取值范围是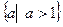 ……………………………………14分
……………………………………14分
练习册系列答案
相关题目
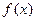 满足:对定义域内任意两个不相等的实数
满足:对定义域内任意两个不相等的实数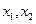 ,都有,则称函数
,都有,则称函数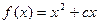 ,且
,且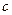 的值;
的值;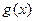 ,并说明理由.
,并说明理由.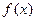 的边际函数为
的边际函数为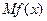 ,定义为
,定义为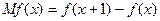 ,某服
,某服 件的收入函数为
件的收入函数为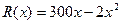 (单位元),其成本函数为
(单位元),其成本函数为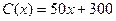 (单位元),利润等于收入与成本之差.
(单位元),利润等于收入与成本之差.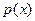 及其边际利润函数
及其边际利润函数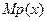 ;
;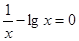 必有一个根的区间是( )
必有一个根的区间是( )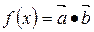 ,其中向量
,其中向量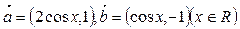
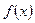 的最小正周期;
的最小正周期;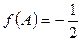 ,且
,且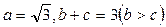 ,求
,求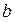 与
与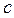 的值。
的值。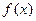 是定义在
是定义在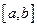 上的函数,其图像是一条连续的曲线,且满足下列条件:
上的函数,其图像是一条连续的曲线,且满足下列条件: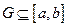 ;
;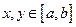 ,都有
,都有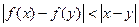 .
.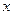 的方程
的方程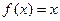 在区间
在区间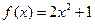 ,值域为
,值域为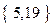 的“孪生函数”共有_______个.
的“孪生函数”共有_______个.