题目内容
(本小题14分)
某市的一家报刊摊点,从报社买进《晚报》的价格是每份0.20元,卖出价是每份0.30元,卖不掉的报纸可以以每份0.05元价格退回报社.在一个月(以30天计)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使每月所获的利润最大?并计算他一个月最多可赚得多少元?
某市的一家报刊摊点,从报社买进《晚报》的价格是每份0.20元,卖出价是每份0.30元,卖不掉的报纸可以以每份0.05元价格退回报社.在一个月(以30天计)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天从报社买进的份数必须相同,这个摊主每天从报社买进多少份,才能使每月所获的利润最大?并计算他一个月最多可赚得多少元?
当x = 400时,y有最大值825元
解 设摊主每天从报社买进x份,显然当x∈[250,400]时,每月所获利润才能最大.
于是每月所获利润y为 ( 4分 )
y =20·0.30x+10·0.30·250+10·0.05·(x-250)-30·0.20x
=0.5x+625,x∈[250,400]. ( 5分 )
因函数y在[250,400]上为增函数,
故当x = 400时,y有最大值825元. ( 5分 )
于是每月所获利润y为 ( 4分 )
y =20·0.30x+10·0.30·250+10·0.05·(x-250)-30·0.20x
=0.5x+625,x∈[250,400]. ( 5分 )
因函数y在[250,400]上为增函数,
故当x = 400时,y有最大值825元. ( 5分 )

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
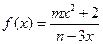 是定义域上的奇函数,且
是定义域上的奇函数,且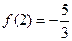 ;函数
;函数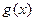 是
是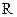 上的增函数,
上的增函数,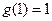 且对任意
且对任意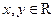 ,总有
,总有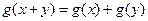
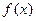 的解析式;
的解析式;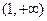 上的单调性,并加以证明;
上的单调性,并加以证明;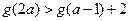 ,求实数
,求实数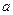 的取值范围.
的取值范围.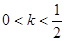 时,方程
时,方程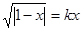 的解的个数是
的解的个数是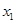 是方程
是方程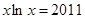 的根,
的根,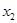 是方程
是方程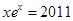 的根,则下列关于
的根,则下列关于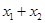 B.
B. 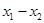 C.
C. 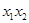 D.
D. 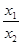
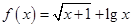 的定义域是 ( )
的定义域是 ( )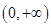
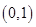
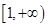
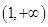
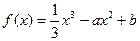 在
在 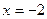 处有极值。
处有极值。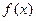 的单调区间;
的单调区间;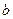 的取值范围。
的取值范围。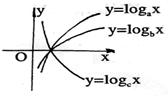
 b
b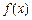 满足:①定义域为
满足:①定义域为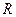 ;②对任意
;②对任意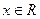 ,有
,有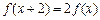 ;③当
;③当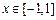
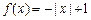 .则方程
.则方程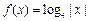 在区间
在区间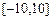 内的解的个数是 .
内的解的个数是 .