题目内容
已知函数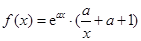 ,其中
,其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求f(x)的单调区间.
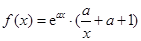 ,其中
,其中 .
.(Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(Ⅱ)求f(x)的单调区间.
(Ⅰ)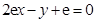 (Ⅱ)① 当
(Ⅱ)① 当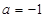 时, 单调递减区间为
时, 单调递减区间为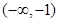 ;单调递增区间为
;单调递增区间为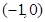 ,
,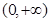 .②当
.②当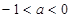 时,
时,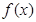 的单调递减区间为
的单调递减区间为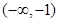 ,
,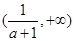 ;单调递增区间为
;单调递增区间为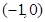 ,
,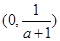 ③ 当
③ 当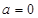 时,
时,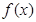 为常值函数,不存在单调区间.④当
为常值函数,不存在单调区间.④当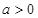 时,
时,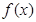 的单调递减区间为
的单调递减区间为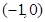 ,
,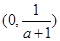 ;单调递增区间为
;单调递增区间为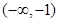 ,
,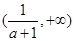 .
.
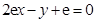 (Ⅱ)① 当
(Ⅱ)① 当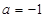 时, 单调递减区间为
时, 单调递减区间为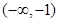 ;单调递增区间为
;单调递增区间为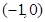 ,
,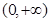 .②当
.②当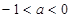 时,
时,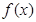 的单调递减区间为
的单调递减区间为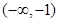 ,
,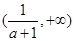 ;单调递增区间为
;单调递增区间为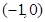 ,
,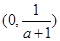 ③ 当
③ 当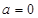 时,
时,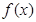 为常值函数,不存在单调区间.④当
为常值函数,不存在单调区间.④当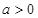 时,
时,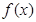 的单调递减区间为
的单调递减区间为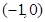 ,
,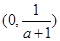 ;单调递增区间为
;单调递增区间为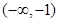 ,
,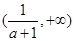 .
.(Ⅰ)解:当 时,
时,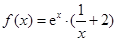 ,
,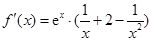 .………………2分
.………………2分
由于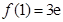 ,
,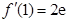 ,
,
所以曲线 在点
在点 处的切线方程是
处的切线方程是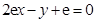 . ………………4分
. ………………4分
(Ⅱ)解: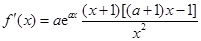 ,
, . ………………6分
. ………………6分
① 当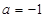 时,令
时,令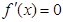 ,解得
,解得 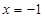 .
.
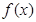 的单调递减区间为
的单调递减区间为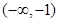 ;单调递增区间为
;单调递增区间为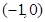 ,
,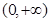 .……………8分
.……………8分
当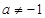 时,令
时,令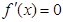 ,解得
,解得 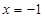 ,或
,或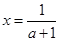 .
.
② 当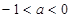 时,
时,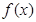 的单调递减区间为
的单调递减区间为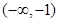 ,
,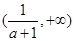 ;单调递增区间为
;单调递增区间为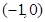 ,
,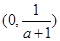 ………………10分
………………10分
③ 当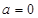 时,
时,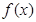 为常值函数,不存在单调区间.………………11分
为常值函数,不存在单调区间.………………11分
④ 当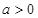 时,
时,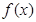 的单调递减区间为
的单调递减区间为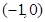 ,
,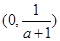 ;单调递增区间为
;单调递增区间为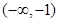 ,
,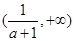 .………………13分
.………………13分
 时,
时,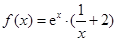 ,
,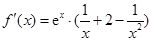 .………………2分
.………………2分由于
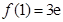 ,
,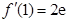 ,
,所以曲线
 在点
在点 处的切线方程是
处的切线方程是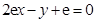 . ………………4分
. ………………4分(Ⅱ)解:
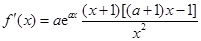 ,
, . ………………6分
. ………………6分① 当
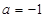 时,令
时,令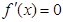 ,解得
,解得 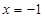 .
.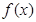 的单调递减区间为
的单调递减区间为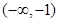 ;单调递增区间为
;单调递增区间为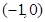 ,
,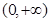 .……………8分
.……………8分当
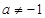 时,令
时,令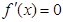 ,解得
,解得 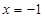 ,或
,或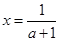 .
.② 当
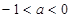 时,
时,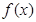 的单调递减区间为
的单调递减区间为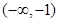 ,
,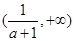 ;单调递增区间为
;单调递增区间为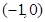 ,
,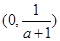 ………………10分
………………10分③ 当
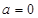 时,
时,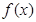 为常值函数,不存在单调区间.………………11分
为常值函数,不存在单调区间.………………11分④ 当
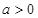 时,
时,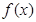 的单调递减区间为
的单调递减区间为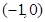 ,
,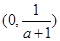 ;单调递增区间为
;单调递增区间为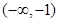 ,
,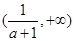 .………………13分
.………………13分
练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
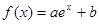 在
在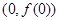 处切线为
处切线为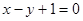 .
. 的解析式;
的解析式; ,
, ,
,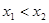 ,
,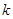 表示直线
表示直线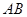 的斜率,求证:
的斜率,求证: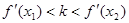 .
.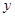 (升)与行驶速度
(升)与行驶速度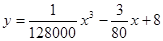 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。 的导数
的导数 ,则数列
,则数列 的前n项和( )
的前n项和( )



 在
在 处的切线方程是( )
处的切线方程是( )



 作函数y=f(x)图象的切线,则切线的方程为________.
作函数y=f(x)图象的切线,则切线的方程为________. ,且f(x)的图象在x=1处与直线y=2相切.
,且f(x)的图象在x=1处与直线y=2相切.



 在点P(3,1)处的切线斜率为 ( ).
在点P(3,1)处的切线斜率为 ( ).