题目内容
20.如果对任意一个三角形,只要它的三边a,b,c都在函数f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“和美型函数”.现有下列函数:①f(x)=$\sqrt{x}$; ②g(x)=sinx,x∈(0,π); ③φ(x)=2x;④h(x)=lnx,x∈[2,+∞).其中是“和美型函数”的函数序号为①④.(写出所有正确的序号)分析 ①由0<a≤b≤c,且a+b>c,判断$\sqrt{a}$+$\sqrt{b}$>$\sqrt{c}$成立即可;
②举例说明y=sinx不是“和美型函数”;
③举例说明y=2x不是“和美型函数”;
④由2≤a≤b<c,说明lna+lnb>lnc成立即可.
解答 解:对于①,设0<a≤b≤c,且a+b>c,欲证明$\sqrt{a}$+$\sqrt{b}$>$\sqrt{c}$,
只需证明a+b+2$\sqrt{ab}$>c,即2$\sqrt{ab}$>0成立;∴①是“和美型函数”;
对于②,取a=$\frac{π}{2}$,b=$\frac{5π}{6}$,c=$\frac{5π}{6}$,而sinb+sinc=sina,∴②不是“和美型函数”;
对于③,取a=2,b=2,c=3,则22+22=23,∴以22、22、23为三边不能构成三角形,
③不是“和美型函数”;
对于④,设2≤a≤b<c,此时只需证lna+lnb>lnc,即证lnab>lnc,即证ab>c,
由①知a+b>c,而ab-(a+b)=ab-a-b+1-1=(a-1)(b-1)-1≥0,即ab≥a+b>c,
∴lna+lnb>lnc成立,即h(x)=lnx,x∈[2,+∞)是“和美型函数”.
综上,是“和美型函数”的函数序号为①④.
故答案为:①④.
点评 本题考查了新定义的函数的性质与应用问题,也考查了综合分析问题与解决问题的能力,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.阅读如图的程序框图,则输出的S( )
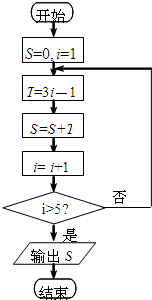

| A. | 6 | B. | 14 | C. | 26 | D. | 40 |
15.已知集合A={y|y=x2+2x-3},$B=\left\{{\left.y\right|y=x+\frac{1}{x},x>0}\right\}$,则有( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=φ |
5.若a>b,则下列不等式成立的是( )
| A. | algx>blgx(x>0) | B. | ax2>bx2 | C. | a2>b2 | D. | $\frac{a}{{{2^x}+1}}>\frac{b}{{{2^x}+1}}$ |
9.圆x2+y2+2x-2y+1=0关于直线x-y+3=0对称圆的方程为( )
| A. | (x-1)2+(y+1)2=1 | B. | (x+2)2+(y-2)2=1 | C. | (x+1)2+(y-1)2=1 | D. | (x-2)2+(y+2)2=1 |