题目内容
(本小题满分17分)已知点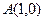 ,
,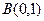 和互不相同的点
和互不相同的点 ,满足
,满足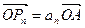
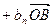
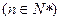 ,其中
,其中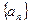 、
、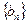 分别为等差数列和等比数列,
分别为等差数列和等比数列,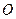 为坐标原点,
为坐标原点,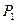 是线段
是线段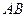 的中点.
的中点.
(1) 求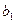 ,
,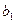 的值;
的值;
(2) 点 能否在同一条直线上?证明你的结论;
能否在同一条直线上?证明你的结论;
(3) 证明:对于给定的公差不为零的数列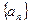 ,都能找到惟一的数列
,都能找到惟一的数列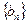 ,使得
,使得 都在一个指数函数的图象上.
都在一个指数函数的图象上.
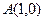 ,
,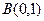 和互不相同的点
和互不相同的点 ,满足
,满足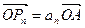
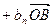
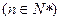 ,其中
,其中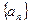 、
、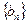 分别为等差数列和等比数列,
分别为等差数列和等比数列,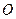 为坐标原点,
为坐标原点,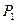 是线段
是线段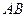 的中点.
的中点.(1) 求
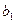 ,
,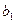 的值;
的值;(2) 点
 能否在同一条直线上?证明你的结论;
能否在同一条直线上?证明你的结论;(3) 证明:对于给定的公差不为零的数列
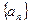 ,都能找到惟一的数列
,都能找到惟一的数列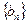 ,使得
,使得 都在一个指数函数的图象上.
都在一个指数函数的图象上.(1) 
(2)见解析
(3)见解析

(2)见解析
(3)见解析
(1)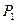 是线段
是线段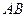 的中点
的中点 . (2分)
. (2分)
又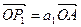
 ,且
,且 不共线,由平面向量基本定理,知
不共线,由平面向量基本定理,知 (4分)
(4分)
(2)由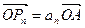
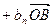
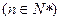
 .由
.由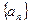 的公差为
的公差为 ,
,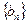 的公比为
的公比为 ,则由于
,则由于 互不相同,所以
互不相同,所以 不会同时成立. (5分)
不会同时成立. (5分)
若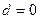 时,则
时,则 ,
,
 都在直线
都在直线 上; (6分)
上; (6分)
若 时,则
时,则 ,
,
 都在直线
都在直线 上; (7分)
上; (7分)
若 ,点
,点 在同一条直线上
在同一条直线上 与
与
 共线 (9分)
共线 (9分)

 )(
)(

 )(
)( )
)
 (
( )-
)- (
( )
)

 =
=

 与
与 矛盾,所以当
矛盾,所以当 时,
时,  不在同一条直线上. (11分)
不在同一条直线上. (11分)
(3)由 (12分)
(12分)
设 ,则
,则 , 点
, 点 都在一指数函数的图象上
都在一指数函数的图象上 且
且

 ,
,  (15分)
(15分)
所以,对于给定的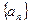 ,都能找到惟一的一个数列
,都能找到惟一的一个数列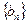 ,
, ,使得
,使得 都在指数函数
都在指数函数 的图象上. (17分)
的图象上. (17分)
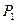 是线段
是线段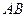 的中点
的中点 . (2分)
. (2分)又
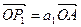
 ,且
,且 不共线,由平面向量基本定理,知
不共线,由平面向量基本定理,知 (4分)
(4分)(2)由
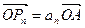
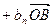
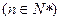
 .由
.由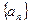 的公差为
的公差为 ,
,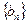 的公比为
的公比为 ,则由于
,则由于 互不相同,所以
互不相同,所以 不会同时成立. (5分)
不会同时成立. (5分)若
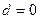 时,则
时,则 ,
,
 都在直线
都在直线 上; (6分)
上; (6分)若
 时,则
时,则 ,
,
 都在直线
都在直线 上; (7分)
上; (7分)若
 ,点
,点 在同一条直线上
在同一条直线上 与
与
 共线 (9分)
共线 (9分)
 )(
)(

 )(
)( )
)
 (
( )-
)- (
( )
)

 =
=

 与
与 矛盾,所以当
矛盾,所以当 时,
时,  不在同一条直线上. (11分)
不在同一条直线上. (11分)(3)由
 (12分)
(12分) 设
 ,则
,则 , 点
, 点 都在一指数函数的图象上
都在一指数函数的图象上 且
且
 ,
,  (15分)
(15分)所以,对于给定的
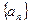 ,都能找到惟一的一个数列
,都能找到惟一的一个数列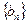 ,
, ,使得
,使得 都在指数函数
都在指数函数 的图象上. (17分)
的图象上. (17分)
练习册系列答案
相关题目
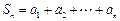 ,且
,且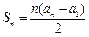 .
.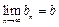 ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令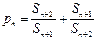 ,求数列
,求数列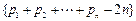 的“上渐近值”.
的“上渐近值”.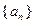 的公差是
的公差是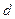 ,
,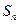 是该数列的前
是该数列的前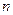 项和.
项和.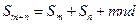 ;
;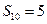 、
、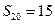 ,求
,求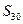 ”;
”;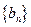 的公比为
的公比为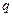 ,前
,前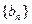 ,其中
,其中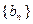 的前
的前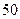 项和
项和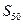 .”
.”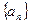 满足
满足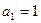 ,
,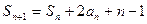 .
.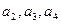 ;
;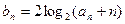 ,设
,设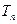 是数列
是数列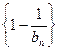 的前
的前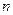 项积,若
项积,若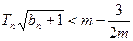 对
对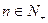 恒成立,求实数m的范围。
恒成立,求实数m的范围。 的通项公式
的通项公式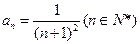 ,
, 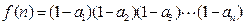 ,
,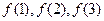 的值,由此推测
的值,由此推测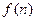 的计算公式,并用数学归纳法加以证明.
的计算公式,并用数学归纳法加以证明.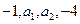 成等差数列,
成等差数列,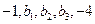 成等比数列,则
成等比数列,则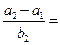 ( )
( )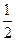



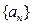 前n项和为
前n项和为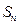 ,且
,且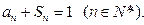
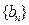 满足
满足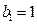 且
且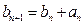 (n≥1),求数列
(n≥1),求数列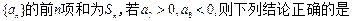 ( )
( )


