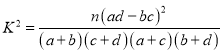题目内容
【题目】如图，椭圆
的左、右焦点分别为
，
.已知点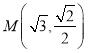
在椭圆上，且点M到两焦点距离之和为4.
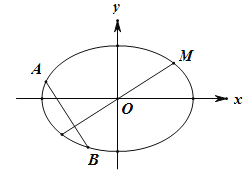
（1）求椭圆的方程；
（2）设与MO（O为坐标原点）垂直的直线交椭圆于A，B（A，B不重合），求
的取值范围.
【答案】（1）
（2）
【解析】
（1）由M到两焦点距离之和为4可得a，再将M代入方程可得b即可得到椭圆方程；
（2）由已知可设AB的方程为
，
，
联立椭圆方程得到根与系数的关系，以及m的范围，将其代入
中计算即可得到答案.
解：（1）∵椭圆
的左、右焦点分别为
，
.
点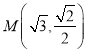
在椭圆上，且点M到两焦点距离之和为4，
∴
，
，∴椭圆方程为
，
把点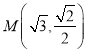代入，得
，解得
，
∴椭圆的方程为.
（2）∵
，
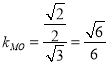与MO（O为坐标原点）垂直的直线交椭圆于A，B（A，B不重合），
∴设AB的方程为，
联立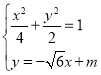
，消去y，得：
，
，
解得
，∴
，
设，，则
，
，
∴
，
∴求
的取值范围是.
【点晴】
本题考查直线与椭圆的位置关系，涉及到向量的数量积的运算，考查学生数学运算能力，是一道中档题.
【题目】2020年初，由于疫情影响，开学延迟，为了不影响学生的学习，国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”，某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类，且这两类学习互不影响已知其积分规则如下：每阅读一篇文本资料积1分，每日上限积5分;观看视频1个积2分，每日上限积6分．经过抽样统计发现，文本资料学习积分的概率分布表如表1所示，视频资料学习积分的概率分布表如表2所示．
表1
文本学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
（1）现随机抽取1人了解学习情况，求其每日学习积分不低于9分的概率；
（2）现随机抽取3人了解学习情况，设积分不低于9分的人数为
，求
的分布列及数学期望．
【题目】在疫情这一特殊时期，教育行政部门部署了“停课不停学”的行动，全力帮助学生在线学习.复课后进行了摸底考试，某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系，对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的，得到了如下的等高条形图：
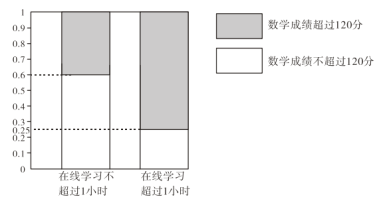
（Ⅰ）是否有
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”；
（Ⅱ）将频率视为概率，从全校高三学生这次数学成绩超过120分的学生中随机抽取10人，求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
