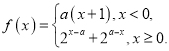题目内容
【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.
表1
文本学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ;(2)分布列详见解析,数学期望为
;(2)分布列详见解析,数学期望为![]() .
.
【解析】
(1)由题意可得获得的积分不低于(9分)的情形,因为两类学习互不影响,根据相互独立与互斥事件的概率计算公式即可得出概率![]() .
.
(2)随机变量![]() 的所有可能取值为0,1,2,3.由(1)每个人积分不低于(9分)的概率为
的所有可能取值为0,1,2,3.由(1)每个人积分不低于(9分)的概率为![]() .根据二项分布列的概率计算公式即可得出.
.根据二项分布列的概率计算公式即可得出.
(1)由题意,获得的积分不低于9分的情形共有(如下表所示):
文本 | 3 | 4 | 5 | 5 |
视频 | 6 | 6 | 6 | 4 |
因为两类学习情况互不影响,
所以每日学习积分不低于9分的概率![]() ,
,
即每日学习积分不低于9分的概率为![]() .
.
(2)随机变量![]() 的所有可能取值为0,1,2,3
的所有可能取值为0,1,2,3
由(1)每个人积分不低于9分的概率为![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以随机变量![]() 的概率分布列为:
的概率分布列为:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
可得![]() .
.
所以随机变量![]() 的数学期望为
的数学期望为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某厂家准备在“6.18”举行促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出.广告费支出x(万元)和销售量y(万台)的数据如下:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售量y | 1.8 | 3.0 | 4.0 | 4.2 | 5.0 | 5.3 | 5.4 |
(1)若用线性回归模型拟合y与x的关系,求出y关于x的线性回归方程(保留小数点后两位);
(2)若用![]() 模型拟合y与x的关系,可得回归方程
模型拟合y与x的关系,可得回归方程![]() ,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
,经计算线性回归模型和该模型的R2分别约为0.774和0.888,请用R2说明选择哪个回归模型更好;
(3)已知利润z与x,y的关系为z=200y-x.根据(2)的结果,当广告费x=20时,求销售量及利润的预报值.
参考公式:回归直线![]() =
=![]() +
+![]() x的斜率和截距的最小二乘估计分别为
x的斜率和截距的最小二乘估计分别为![]() =
=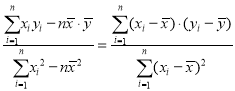 ,
,![]() .
.
参考数据:![]() ≈2.24,
≈2.24,![]() ,
, ![]()
【题目】在对人们休闲方式的一次调查中,共调查120人,其中女性70人,男性50人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动.
(1)请画出性别与休闲方式的![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.10的前提下,认为休闲方式与性别有关?
附: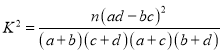 ,
,
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |