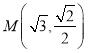题目内容
【题目】已知函数![]() 为
为![]() 上的偶函数,
上的偶函数,![]() 为
为![]() 上的奇函数,且
上的奇函数,且![]() .
.
(1)求![]() 和
和![]() 的表达式;
的表达式;
(2)判断并证明![]() 的单调性;
的单调性;
(3)若存在![]() 使得不等式
使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 在
在![]() 上单调递增,证明见解析;(3)
上单调递增,证明见解析;(3)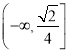 .
.
【解析】
(1)根据函数的奇偶性列出两个方程,解出即可;
(2)根据函数单调性的定义,取值、作差、变形、定号、下结论即可证出;
(3)先将不等式![]() 化为
化为![]() ,再换元,
,再换元,
令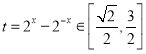 ,然后分参转化为
,然后分参转化为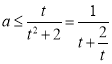 ,最后求出
,最后求出![]() 的最大值,即得实数
的最大值,即得实数![]() 的取值范围.
的取值范围.
(1)因为![]() ①,将
①,将![]() 换为
换为![]() ,代入上式得
,代入上式得![]() ,
,
由于![]() 是偶函数,
是偶函数,![]() 是奇函数,所以
是奇函数,所以![]() ,
,![]() ,
,
即![]() ②,
②,
由①②可解得,![]() ,
,![]() .
.
(2)![]() 在
在![]() 上单调递增.
上单调递增.
证明如下:任取![]() 且
且![]() ,
,
![]() ,
,
因为当![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
(3)由题意可得![]() ,
,
令![]() ,由
,由![]() 可得
可得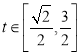 ,则
,则![]() ,
,
即原命题等价于存在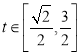 使得
使得![]() 成立,
成立,
分离参变量得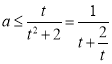 ,只需
,只需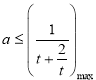 即可.
即可.
又因为![]() ,所以
,所以![]() ,即
,即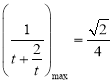 ,
,
所以,实数![]() 的取值范围为
的取值范围为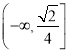 .
.

练习册系列答案
相关题目
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|