题目内容
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
【答案】(1)V(r)=![]() (300r﹣4r3) (0,5
(300r﹣4r3) (0,5![]() )
)
(2)见解析
【解析】
试题(1)先由圆柱的侧面积及底面积计算公式计算出侧面积及底面积,进而得出总造价,依条件得等式![]() ,从中算出
,从中算出![]() ,进而可计算
,进而可计算![]() ,再由
,再由![]() 可得
可得![]() ;(2)通过求导
;(2)通过求导![]() ,求出函数
,求出函数![]() 在
在![]() 内的极值点,由导数的正负确定函数的单调性,进而得出
内的极值点,由导数的正负确定函数的单调性,进而得出![]() 取得最大值时
取得最大值时![]() 的值.
的值.
(1)∵蓄水池的侧面积的建造成本为![]() 元,底面积成本为
元,底面积成本为![]() 元
元
∴蓄水池的总建造成本为![]() 元
元
所以即![]()
∴![]()
∴![]()
又由![]() 可得
可得![]()
故函数![]() 的定义域为
的定义域为![]() 6分
6分
(2)由(1)中![]() ,
,![]()
可得![]() (
(![]() )
)
令![]() ,则
,则![]()
∴当![]() 时,
时,![]() ,函数
,函数![]() 为增函数
为增函数
当![]() ,函数
,函数![]() 为减函数
为减函数
所以当![]() 时该蓄水池的体积最大 12分.
时该蓄水池的体积最大 12分.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各![]() 人,甲班按原有模式教学,乙班实施教学方法改革,经过一年的教学,将甲、乙两个班学生一年来的数学成绩取整数,绘制成如下茎叶图,规定不低于
人,甲班按原有模式教学,乙班实施教学方法改革,经过一年的教学,将甲、乙两个班学生一年来的数学成绩取整数,绘制成如下茎叶图,规定不低于![]() 分(百分制)为优秀,甲班同学成绩的中位数为
分(百分制)为优秀,甲班同学成绩的中位数为![]() .
.

(1)求![]() 的值和乙班同学成绩的众数;
的值和乙班同学成绩的众数;
(2)完成表格,若有![]() 以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大教学改革面?说明理由.
以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大教学改革面?说明理由.
甲班 | 乙班 | 合计 | |
优秀人数 | |||
不优秀人数 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
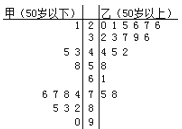
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |