题目内容
1.若函数y=k(x+1)的图象上存在点(x,y)满足约束条件$\left\{\begin{array}{l}{x-y+\sqrt{3}≥0}\\{\sqrt{3}x-y-\sqrt{3}≤0}\\{y≥\sqrt{3}}\end{array}\right.$,则函数y=k(x+1)的图象与圆(x-4)2+(y-3)2=2有公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
分析 由题意画出约束条件的区域,计算函数y=k(x+1)的图象与圆(x-4)2+(y-3)2=2有公共点可能,利用几何概型公式解答.
解答  解:由约束条件$\left\{\begin{array}{l}{x-y+\sqrt{3}≥0}\\{\sqrt{3}x-y-\sqrt{3}≤0}\\{y≥\sqrt{3}}\end{array}\right.$,作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{x-y+\sqrt{3}≥0}\\{\sqrt{3}x-y-\sqrt{3}≤0}\\{y≥\sqrt{3}}\end{array}\right.$,作出可行域如图,
直线y=k(x+1)过定点P(-1,0),
由图可知A(2,$\sqrt{3}$),B(0,$\sqrt{3}$),
则kPA=$\frac{\sqrt{3}}{3}$,kPB=$\sqrt{3}$,
∴$\frac{\sqrt{3}}{3}≤k≤\sqrt{3}$,
函数y=k(x+1)的图象与圆(x-4)2+(y-3)2=2有公共点,则$\frac{|k(4+1)-3|}{\sqrt{{k}^{2}+1}}$≤$\sqrt{2}$,解得$\frac{7}{23}$≤k≤1,
∵$\frac{\sqrt{3}}{3}≤k≤\sqrt{3}$,
∴$\frac{\sqrt{3}}{3}$≤k≤1,
∴函数y=k(x+1)的图象与圆(x-4)2+(y-3)2=2有公共点的概率为:$\frac{1-\frac{\sqrt{3}}{3}}{\sqrt{3}-\frac{\sqrt{3}}{3}}$=$\frac{\sqrt{3}-1}{2}$.
故选:C.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.2014年夏天,云南省鲁甸县发生6.5级地震,造成许多人员伤亡.某医院迅速组织了甲、乙两个医疗队到鲁甸县去抗震救灾.甲、乙两个医疗队的人员分布情况如表.鲁甸县的某乡村由于地理位置偏远,当地医疗人员少且医疗技术落后,故要利用分层抽样的方法在甲、乙两队中各选3名医生到该乡村帮助当地医疗人员救护受伤人员.
(1)求从甲队中抽取的医生中至少有1名是女医生的概率;
(2)记X表示抽取到男医生的人数,求X的分布列及数学期望.
| 医疗队\性别 | 男医生 | 女医师 |
| 甲 | 6 | 4 |
| 乙 | 3 | 2 |
(2)记X表示抽取到男医生的人数,求X的分布列及数学期望.
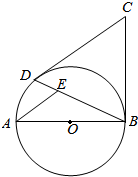 如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.
如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.