题目内容
6.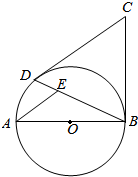 如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.
如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.
分析 连结CO、DO、AD,设CO交BD于F,由切线性质和弦切角定理推导出△CDF≌△BDA,由此利用勾股定理和二倍角公式能求出sin∠BAE.
解答  解:连结CO、DO、AD,设CO交BD于F,
解:连结CO、DO、AD,设CO交BD于F,
∵切线CD、切线CB分别与⊙O相交于点D、B,
AB为⊙O的直径,AE∥CD交BD于点E,AB=BC,
∴CO⊥BD,AB⊥CB,AD⊥BD,CD⊥OD,OD⊥AE,
∴CB=2OB,∠CDB=∠BAD,AB=CD,
∴△CDF≌△BDA,∴AD=DF=BF,
∴∠BDO=∠ABD,∠AOD=2∠ABD,
设AD=DF=BF=a,则$AB=\sqrt{{a}^{2}+4{a}^{2}}$=$\sqrt{5}a$,
∴sin∠ABD=$\frac{AD}{AB}$=$\frac{1}{\sqrt{5}}$,cos∠ABD=$\frac{BD}{AB}$=$\frac{2}{\sqrt{5}}$,
∴cos∠AOD=cos2∠ABD=1-2sin2∠ABD=1-2×$\frac{1}{5}$=$\frac{3}{5}$,
∴sin∠BAE=cos$∠AOD=\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查角的正弦值的求法,是中档题,解题时要认真审题,注意弦切角定理、切线性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.若函数y=k(x+1)的图象上存在点(x,y)满足约束条件$\left\{\begin{array}{l}{x-y+\sqrt{3}≥0}\\{\sqrt{3}x-y-\sqrt{3}≤0}\\{y≥\sqrt{3}}\end{array}\right.$,则函数y=k(x+1)的图象与圆(x-4)2+(y-3)2=2有公共点的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{3}+1}{4}$ |