题目内容
6. 将正奇数组成的数列{an},按下表排成5列:
将正奇数组成的数列{an},按下表排成5列:| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | … | … | 27 | 25 |
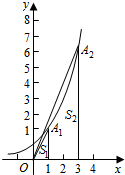
(Ⅱ)已知点A1(a1,b1),A2(a2,b2),…,An(an,bn)在指数函数y=2x的图象上,如果,以A1,A2,…,An为一个顶点,x轴y轴为邻边构成的矩形面积为S1,S2,…Sn,求S1+S2+…+Sn的值Tn.
分析 (Ⅰ)因为{an}为等差数列,故an=1+(n-1)×2=2n-1,第五行的第一个数为a17=1+(17-1)×2=33,由此推出结论.
(Ⅱ)将点An(an,bn)代入函数y=2x,利用乘公比错位相减求得Tn
解答 解:(Ⅰ)因为{an}为等差数列,故an=1+(n-1)×2=2n-1,第五行的第一个数为a17=1+(17-1)×2=33
第十行的最后一个数为a10=1+(40-1)×2=79,
故第五行到第十行的所有数字的和为33+35+…+79=$\frac{24(33+79)}{2}=1344$
(Ⅱ)因为An(an,bn)在函数y=2x图象上,故bn=2an=22n-1,又因为an=2n-1,故S1=a1b1=2,S2=a2b2=3×23=24,Sn=anbn=(2n-1)×2 2n-1,
所以${T}_{n}={S}_{1}+{S}_{2}+…+{S}_{n}=1×2+3×{2}^{3}$+…+(2n-1)×22n-1①
$4{T}_{n}=1×{2}^{3}+3×{2}^{5}+…+(2n-3){2}^{2n-1}$+…+(2n-1)22n-3②
①-②得-3Tn=2+2(23+25+…+22n-1)-(2n-1)×22n-3
=2(2+(2+23+25+…+22n-1)-(2n-1)×22n-1
=$2\frac{2(1-{4}^{n})}{1-4}-2=(2n-1){2}^{2n+1}$
=$(\frac{10}{3}-4n)×{4}^{n}-\frac{10}{3}$
故$Tn=(\frac{4n}{3}-\frac{10}{9})×{4}^{n}+\frac{10}{9}$
点评 本题主要考查乘公比错位相减的方法,属于中档题型,高考经常涉及此考点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.某程序框图如图所示,该程序运行后,输出的x值为15,则a等于( )

| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
11.如图所示的程序框图,若输入$x=\frac{1}{2}$,则输出的结果S=( )


| A. | $\sqrt{2}$ | B. | $\frac{1}{4}$ | C. | -1 | D. | 1 |
15.“函数f(x)=lg(ax+1)在(0,+∞)上单调递增”是“a>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.设集合A={x|x2-1<0},B={x|x+2≥0},则A∩B=( )
| A. | {x|-1<x<1} | B. | {x|x≥-2} | C. | {x|-2≤x<1} | D. | {x|-1<x≤2} |