题目内容
【题目】已知关于x的函数 ![]() .
.
(1)如果函数 ![]() ,求b、c;
,求b、c;
(2)设当x∈( ![]() ,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
【答案】
(1)解:函数 ![]() 导数为f′(x)=﹣x2+2bx+c,
导数为f′(x)=﹣x2+2bx+c,
函数 ![]() ,可得f(1)=﹣
,可得f(1)=﹣ ![]() ,f′(1)=0,
,f′(1)=0,
即为﹣1+2b+c=0,﹣ ![]() +b+c+bc=﹣
+b+c+bc=﹣ ![]() ,
,
解得b=1,c=﹣1;b=﹣1,c=3.
当b=1,c=﹣1时,f′(x)=﹣x2+2x﹣1=﹣(x﹣1)2≤0,f(x)递减,不满足题意;
当b=﹣1,c=3时,f′(x)=﹣x2﹣2x+3=﹣(x﹣1)(x+3),满足题意.
综上可得,b=﹣1,c=3
(2)解:函数y=f(x)﹣c(x+b)=﹣ ![]() x3+bx2,导数f′(x)=﹣x2+2bx,
x3+bx2,导数f′(x)=﹣x2+2bx,
由题意可得﹣x2+2bx≤2在x∈( ![]() ,3)时恒成立,
,3)时恒成立,
即有2b≤x+ ![]() 的最小值,
的最小值,
由x+ ![]() ≥2
≥2 ![]() =2
=2 ![]() ,当且仅当x=
,当且仅当x= ![]() 时,取得最小值2
时,取得最小值2 ![]() .
.
即有2b≤2 ![]() ,解得b≤
,解得b≤ ![]() ,
,
则b的范围是(﹣∞, ![]() ]
]
【解析】(1)求出函数的导数,由题意可得f(1)=﹣ ![]() ,f′(1)=0,解方程可得b,c,检验是否由极值点;(2)求得函数y=f(x)﹣c(x+b)=﹣
,f′(1)=0,解方程可得b,c,检验是否由极值点;(2)求得函数y=f(x)﹣c(x+b)=﹣ ![]() x3+bx2 , 求出导数,由题意可得2b≤x+
x3+bx2 , 求出导数,由题意可得2b≤x+ ![]() 的最小值,运用基本不等式可得右边函数的最小值,即可得到a的范围.
的最小值,运用基本不等式可得右边函数的最小值,即可得到a的范围.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

【题目】兰州一中在世界读书日期间开展了“书香校园”系列读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”。
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 |
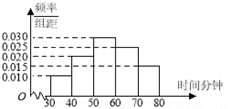
(1)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(2)利用分层抽样从这100名学生的“读书迷”中抽取8名进行集训,从中选派2名参加兰州市读书知识比赛,求至少有一名男生参加比赛的概率。
附: 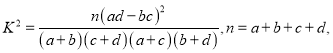
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |