题目内容
11.给出以下命题:①存在两个不等实数α,β,使得等式sin(α+β)=sinα+sinβ成立;
②若数列{an}是等差数列,且am+an=as+at(m、n、s、t∈N*),则m+n=s+t;
③若Sn是等比数列{an}的前n项和,则S6,S12-S6,S18-S12成等比数列;
④若Sn是等比数列{an}的前n项和,且Sn=Aqn+B;(其中A、B是非零常数,n∈N*),则A+B为零;
⑤已知△ABC的三个内角A,B,C所对的边分别为a,b,c,若a2+b2>c2,则△ABC一定是锐角三角形.
其中正确的命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用特殊值判断①的正误;利用特殊数列即可推出命题②的正误;根据等差数列的性质,判断③的正误;根据等比数列的前n项的和推出A,B判断④的正误.利用特殊三角形判断⑤的正误;
解答 解:对于①实数α=0,β≠0,则sin(α+β)=sinβ,sinα+sinβ=sinβ,所以等式成立;故①正确;
对于②取数列{an}为常数列,对任意m、n、s、t∈N*,都有am+an=as+at,故②不正确;
对于③设an=(-1)n,
则S2=0,S4-S2=0,S6-S4=0,
∴此数列不是等比数列,故③不正确;
④Sn是等比数列{an}的前n项和,且Sn=Aqn+B;(其中A、B是非零常数,n∈N*),
所以此数列为首项是a1,公比为q≠1的等比数列,
则Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$,
所以A=$\frac{{a}_{1}}{1-q}$,B=-$\frac{{a}_{1}}{1-q}$,∴A+B=0,故④正确;
对于⑤,如果三角形是直角三角形,a=5,b=3.c=4,满足a2+b2>c2,故⑤不正确;
故选:B.
点评 此题考查学生灵活运用等差、等比数列的性质,三角函数以及三角形的判断,是一道综合题.属中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
1.方程x2+y2+ax+2ay+2a2+a-1=0表示的曲线是圆,则a的取值范围是( )
| A. | R | B. | (-∞,-2)∪($\frac{2}{3}$,+∞) | C. | (-$\frac{2}{3}$,2) | D. | (-2,$\frac{2}{3}$) |
2.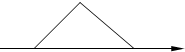 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
6.设集合A={(x,y)||x|+|y|≤1},若动点P(x,y)∈A,则x2+(y-1)2≤2的概率是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | π |
1.从装有红球、黑球和白球的口袋中摸出一个球,若摸出的球是红球的概率是0.4,摸出的球是黑球的概率是0.25,那么摸出的球是白球或黑球的概率是( )
| A. | 0.35 | B. | 0.65 | C. | 0.1 | D. | 0.6 |
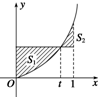 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).