题目内容
16.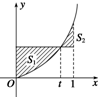 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
分析 首先利用定积分分别求出S1,S2,得到函数g(t),然后分析其单调性.
解答 解:由题意S1=${∫}_{0}^{t}{(t}^{2}-{x}^{2})dx$=(t2x-$\frac{1}{3}{x}^{3}$)|${\;}_{0}^{t}$=$\frac{2}{3}{t}^{3}$,
S2=${∫}_{t}^{1}({x}^{2}-{t}^{2})dx$=($\frac{1}{3}{x}^{3}-{t}^{2}x$)|${\;}_{t}^{1}$=$\frac{1}{3}-{t}^{2}+\frac{2}{3}{t}^{3}$,
所以g(t)=S1+S2=$\frac{4}{3}{t}^{3}-{t}^{2}+\frac{1}{3}$,g'(t)=4t2-2t=2t(2t-1),令g'(t)>0解得t>$\frac{1}{2}$或t<0,又0<t<1,
所以函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1);
故答案为:($\frac{1}{2}$,1).
点评 本题考查了利用定积分求曲边梯形的面积以及利用导数求函数的单调区间;属于经常考查的题型.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.已知集合M={x|(x-1)2≤4}和N={x|x=2k-1,k∈N*},则M∩N=( )
| A. | {1,3} | B. | [1,5) | C. | {1,3,5} | D. | ∅ |
5.下列命题中,假命题为( )
| A. | 存在四边相等的四边形不是正方形 | |
| B. | 设x,y∈R,则“(x-y)•x2<0”是“x<y”的必要而不充分条件 | |
| C. | 若x,y∈R,且x+y>2,则x,y至少有一个大于1 | |
| D. | 命题:?n∈N,2n>1000的否定是:?n∈N,2n≤1000 |
6.已知矩形ABCD,AB=5,BC=7,在矩形ABCD中随机取一点P,则∠APB>90°出现的概率为( )
| A. | $\frac{5π}{56}$ | B. | $\frac{5}{56}$ | C. | $\frac{5π}{28}$ | D. | $\frac{5}{28}$ |