题目内容
已知数列{an}的a1=1,a2=2且an+2=2an+1-an,则a2007=( )
| A.2005 | B.2006 | C.2007 | D.2008 |
∵数列{an}中,an+2=2an+1-an,
∴an+2-an+1=an+1-an,
∴
=1,又a1=1,a2=2,故a2-a1=1,
∴数列{an+1-an}是首项为1,公比为1的等比数列,
∴an+1-an=1,
∴数列{an}是首项为1,公差为1的等差数列,
∴a2007=1+(2007-1)×1=2007.
故选C.
∴an+2-an+1=an+1-an,
∴
| an+2-an+1 |
| an+1-an |
∴数列{an+1-an}是首项为1,公比为1的等比数列,
∴an+1-an=1,
∴数列{an}是首项为1,公差为1的等差数列,
∴a2007=1+(2007-1)×1=2007.
故选C.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
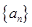 中,若
中,若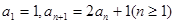
 ,设
,设 ,
, 是等比数列;
是等比数列;