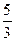题目内容
已知数列{an}的前n项和为Sn.且满足a1=
,an=-2SnSn-1(n≥2)
(1)证明:数列{
}为等差数列;
(2)求Sn及an.
| 1 |
| 2 |
(1)证明:数列{
| 1 |
| Sn |
(2)求Sn及an.
解(1)当n≥2时,an=Sn-Sn-1=-2Sn•Sn-1,
∴
-
=2(n≥2),
∴{
}是以
=
=2为首项,2为公差的等差数列.
(2)∵数列{
}为等差数列,
∴
=2+2(n-1)=2n,
即Sn=
.
当n≥2时,an=Sn-Sn-1=
(
-
)=-
,
∴an=
.
∴
| 1 |
| Sn |
| 1 |
| Sn-1 |
∴{
| 1 |
| Sn |
| 1 |
| S1 |
| 1 |
| a1 |
(2)∵数列{
| 1 |
| Sn |
∴
| 1 |
| Sn |
即Sn=
| 1 |
| 2n |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n-1 |
| 1 |
| 2n(n-1) |
∴an=
|
|

练习册系列答案
相关题目
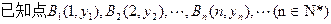
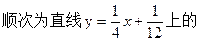 点,点A1(x1,0),A2(x
点,点A1(x1,0),A2(x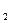 ,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x
,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x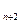 - x
- x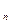 是常数,并求数列{ x
是常数,并求数列{ x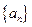 是一个公差为
是一个公差为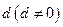 的等差数列,它的前
的等差数列,它的前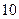 项和
项和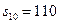 且
且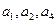 成等比数列,(1)证明
成等比数列,(1)证明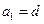 ;(2)求公差
;(2)求公差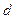 的值和数列
的值和数列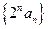 的前
的前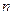 项和
项和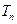 .
.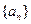 的前n项和为
的前n项和为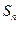 ,且
,且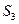 =6,
=6,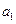 =4, 则公差d等于( )
=4, 则公差d等于( )