题目内容
【题目】已知函数![]() ,
,![]() (其中e为自然对数的底数,m、n为常数),函数
(其中e为自然对数的底数,m、n为常数),函数![]() 定义为:对每一个给定的实数x,
定义为:对每一个给定的实数x,
(1)当m、n满足什么条件时,![]() 对所有的实数x恒成立;
对所有的实数x恒成立;
(2)设a、b是两个实数,满足![]() 且m,
且m,![]() 当
当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间
的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间![]() 的长度定义为
的长度定义为![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意得到![]() 恒成立,从而得到
恒成立,从而得到![]() ,结合绝对值不等式,得到答案;(2)分
,结合绝对值不等式,得到答案;(2)分![]() ,
,![]() ,
,![]() 三种情况进行讨论,根据
三种情况进行讨论,根据![]() 和
和![]() 的图像,得到
的图像,得到![]() 的图像,根据函数图像进行分析,得到答案.
的图像,根据函数图像进行分析,得到答案.
(1)因为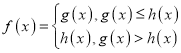 ,
,
所以要得到![]() 对所有的实数x恒成立,
对所有的实数x恒成立,
则![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
则![]() ,取对数得:
,取对数得:![]() 恒成立
恒成立
而![]()
所以![]() 、
、![]() 应满足
应满足![]() ,
,
故![]() 时,
时,![]() 对任意实数x恒成立.
对任意实数x恒成立.
(2)①当![]() 时,
时,![]() ,作出
,作出![]() 和
和![]() 的函数图像,如图
的函数图像,如图![]() 所示,
所示,
根据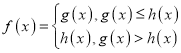 ,可得到
,可得到![]() 图像,如图
图像,如图![]() 所示,
所示,
所以可以得到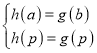 ,
,
即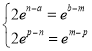 ,即
,即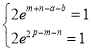 ,
,
所以得到![]() ,
,
![]() ,
,
由图![]() 可知,此时函数
可知,此时函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为
![]()
![]()
![]() ;
;
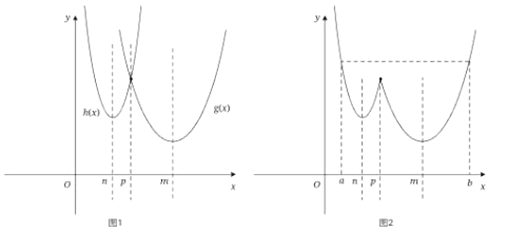
②当![]() 时,
时,![]() ,作出
,作出![]() 和
和![]() 的函数图像,如图
的函数图像,如图![]() 所示,
所示,
根据根据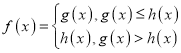 ,可得到
,可得到![]() 图像,如图
图像,如图![]() 所示,
所示,
所以可以得到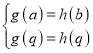 ,
,
即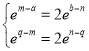 ,即
,即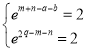 ,
,
所以得到![]() ,
,
![]() ,
,
由图![]() 可知,此时函数
可知,此时函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为
![]()
![]()
![]() ;
;
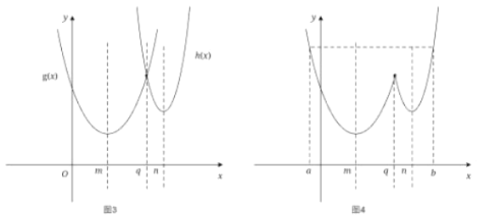
③当![]() 时,由(1)可知,
时,由(1)可知,![]() ,
,
此时![]() 的函数图像关于直线
的函数图像关于直线![]() 对称,如图
对称,如图![]() 所示,
所示,
根据对称性可判断,
此时函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为
![]() ,
,
综上所述,函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为![]() .
.

练习册系列答案
相关题目
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.