Question

【题目】在平面直角坐标系xOy中，已知椭圆C：(a＞b＞0)过点，离心率为.

（1）求椭圆C的方程；

（2）若斜率为的直线l与椭圆C交于A，B两点，试探究是否为定值？若是定值，则求出此定值；若不是定值，请说明理由．

Answer 1

【答案】（1）（2）是定值，7

【解析】

（1）由离心率的值可设椭圆C的方程为，代入点的坐标即可求得c，从而求得椭圆方程；（2）设直线l的方程为y＝x＋n，A(x1，y1)，B(x2，y2)，用x1、x2表示OA2＋OB2，联立直线方程与椭圆方程得到关于x的一元二次方程，韦达定理求出、，代入即可得解.

（1）由离心率，得a∶b∶c＝2∶∶1，

则可设椭圆C的方程为 ，

由点在椭圆C上，得，即c2＝1，

所以椭圆C的方程为

（2）设直线l的方程为y＝x＋n，A(x1，y1)，B(x2，y2)，

所以OA2＋OB2＝＋3－+＋3－＝(＋)＋6.

由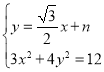消去y得3x2＋2nx＋2n2－6＝0.

当Δ＞0时，x1＋x2＝－n，x1x2＝，

从而＝4，

所以OA2＋OB2＝7，为定值．