题目内容
【题目】如图,四棱锥P﹣ABCD的底面ABCD为直角梯形,AD//BC,且![]() ,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设
,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为等边三角形,M是棱PC上的一点,设![]() (M与C不重合).
(M与C不重合).
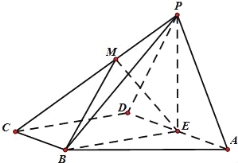
(1)求证:CD⊥DP;
(2)若PA∥平面BME,求k的值;
(3)若二面角M﹣BE﹣A的平面角为150°,求k的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)先证![]() 从而
从而![]() 平面
平面![]() ,进而
,进而![]() 再由
再由![]() 得到
得到![]() ,可证
,可证![]() ;(2)连接
;(2)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() 可得
可得![]() ,从而
,从而![]() ,进而
,进而![]() 求出
求出![]() 的值;(3)连接
的值;(3)连接![]() ,做
,做![]() 交
交![]() 于
于![]() ,做
,做![]() 于
于![]() ,连
,连![]() ,则
,则![]() 为二面角的平面角,进而可求出
为二面角的平面角,进而可求出![]() 的值.
的值.
试题解析:证明:(1)因为△PAD为等边三角形,E为AD的中点,所以PE⊥AD.
因为平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PE![]() 平面PAD,
平面PAD,
所以PE⊥平面ABCD.
又CD![]() 平面ABCD,所以PE⊥CD.
平面ABCD,所以PE⊥CD.
由已知得CD⊥DA,PE∩AD=E,所以CD⊥平面PAD.
双DP![]() 平面PAD,所以CD⊥DP.
平面PAD,所以CD⊥DP.
解:(2)连接AC交BE于N,连接MN.
因为PA∥平面BME,PA![]() 平面PAC,
平面PAC,
平面PAC∩平面BME=MN,所以PA∥MN.
因为AD∥BC,BC⊥DC,所以∠CBN=∠AEN=90°.
又CB=AE,∠CNB=∠ANE,所以△CNB≌△ANE.
所以CN=NA,则M为PC的中点,k=1.
(3)依题意,若二面角M﹣BE﹣A的大小为150°,则二面角M﹣BE﹣C的大小为30°.
连接CE,过点M作MF∥PE交CE于F,过A(0,1,0)作FG⊥BE于G,连接MG.
因为PE⊥平面ABCD,所以MF⊥平面ABCD.
又BE![]() 平面ABCD,所以MF⊥BE.
平面ABCD,所以MF⊥BE.
又MF∩FG=F,MF![]() 平面MFG,FG
平面MFG,FG![]() 平面MFG,
平面MFG,
所以BE⊥平面MFG,从而BE⊥MG.
则∠MGF为二面角M﹣BE﹣C的平面角,即∠MGF=30°.
在等边△PAD中,![]() .由于
.由于![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
在△MFG中,![]()
解得k=3.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
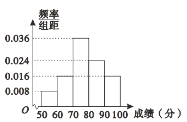
【题目】行了一次水平测试。用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究。经统计成绩的分组及各组的频数如下:![]() ,2;
,2;![]() ,3;
,3;![]() ,10;
,10;![]() ,15;
,15;![]() ,12;
,12;![]() ,8.
,8.
(Ⅰ)频率分布表
分组 | 频数 | 频率 |
| 2 | |
| 3 | |
| 10 | |
| 15 | |
| 12 | |
| 8 | |
合计 | 50 |
频率分布直方图为
(Ⅰ)完成样本的频率分布表;画出频率分直方图;
(Ⅱ)估计成绩在85分以下的学生比例;
(Ⅲ)请你根据以上信息去估计样本的众数、中位数、平均数.(精确到0.01)