题目内容
19.已知数列{an}的前n项和为Sn,Sn=2an-n.(1)证明:{an +1}为等比数列;
(2)证明:$\frac{1}{{a}_{2}-{a}_{1}}$+$\frac{1}{{a}_{3}-{a}_{2}}$+…+$\frac{1}{{a}_{n+1}-{a}_{n}}$<1;
(3)Tn为数列{bn}前n项和,设bn =log2(an +1),是否存在正整数m,k,b${\;}_{k+1}^{2}$=2Tm +19时成立,若存在,求出m,k;若不存在,说明理由.
分析 (1)利用an+1=Sn+1-Sn计算、整理知an+1+1=2(an+1),进而可得结论;
(2)通过(1)可知$\frac{1}{{a}_{n+1}-{a}_{n}}$=$\frac{1}{{2}^{n}}$,利用等比数列的求和公式计算即得结论;
(3)通过an+1=2n可知bn=n、Tn=$\frac{n(n+1)}{2}$,计算即得结论.
解答 (1)证明:∵Sn=2an-n,
∴Sn+1=2an+1-(n+1),
∴an+1=Sn+1-Sn=[2an+1-(n+1)]-(2an-n),
整理得:an+1+1=2(an +1),
又∵a1=S1=2a1-1,即a1+1=1+1=2,
∴数列{an +1}是以首项、公比均为2的等比数列;
(2)证明:由(1)可知an +1=2•2n-1=2n,
∴$\frac{1}{{a}_{n+1}-{a}_{n}}$=$\frac{1}{({2}^{n+1}-1)-({2}^{n}-1)}$=$\frac{1}{{2}^{n}}$,
∴$\frac{1}{{a}_{2}-{a}_{1}}$+$\frac{1}{{a}_{3}-{a}_{2}}$+…+$\frac{1}{{a}_{n+1}-{a}_{n}}$
=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$
=1-$\frac{1}{{2}^{n}}$
<1;
(3)结论:正整数m、k满足题设条件.
理由如下:
∵an+1=2n,
∴bn=log2(an+1)=$lo{g}_{2}{2}^{n}$=n,
∴Tn=$\frac{n(n+1)}{2}$,
假设存在正整数m,k,使得b${\;}_{k+1}^{2}$=2Tm +19成立,
即(k+1)2=2•$\frac{m(m+1)}{2}$+19,
整理得:k(k+2)-m(m+1)=18,
①当k=m时,易知k=m=18;
②当k≠m时,解得k=4、m=2或k=6、m=5;
综上所述:正整数m、k满足题设条件.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | $\stackrel{∧}{y}$=-2x+9.5 | B. | $\stackrel{∧}{y}$=-0.3x+4.2 | C. | $\stackrel{∧}{y}$=0.4x+2.3 | D. | $\stackrel{∧}{y}$=2x-2.4 |
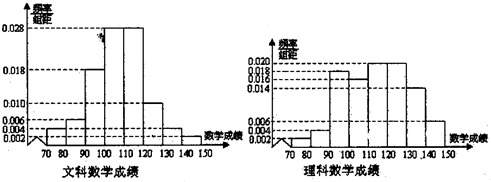
(1)由以上频率分布直方图填写下列2×2列联表,若按是否优秀来判断,是否有99%的把握认为该校的文理科数学成绩有差异.
| 文科 | 理科 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 | 50 | 50 | 100 |
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;
| P(K2>k) | 0.10 | 0.025 | 0.010 |
| K2 | 2.706 | 5.024 | 6.635 |