题目内容

18．已知等差数列{an}的首项a1=20，公差d=-2，则前n项和Sn的最大值为110．

分析 求出等差数列的前n项和，结合一元二次函数的性质进行求解即可．

解答 解：∵等差数列{an}的首项a1=20，公差d=-2，
∴前n项和Sn=20n+$\frac{n（n-1）}{2}$×（-2）=-n2+21n=-（n-$\frac{21}{2}$）2+（$\frac{21}{2}$）2，
则对称轴为n=$\frac{21}{2}$，
∴当n=10或11时，Sn取得最大值，
最大值为S10=-102+21×10=210-100=110，
故答案为：110

点评 本题主要考查等差数列的前n项和公式的应用，结合一元二次函数的性质是解决本题的关键．

练习册系列答案
相关题目
8．某学校为了解该校高三年级学生在市一练考试的数学成绩情况，随机从该校高三文科与理科各抽取50名学生的数学成绩，作出频率分布直方图如图，规定考试成绩[120，150]内为优秀．

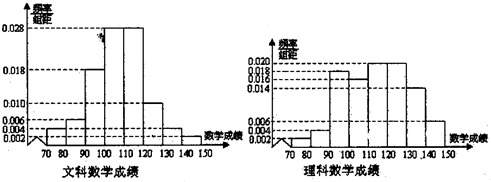
（1）由以上频率分布直方图填写下列2×2列联表，若按是否优秀来判断，是否有99%的把握认为该校的文理科数学成绩有差异．
文科理科总计
优秀
非优秀
总计5050100
（2）某高校派出2名教授对该校随机抽取的学生中一练数学成绩在140分以上的学生进行自主招生面试，每位教授至少面试一人，每位学生只能被一位教授面试，若甲教授面试的学生人数为ξ，求ξ的分布列和数学期望．
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$；
P（K2＞k）0.100.0250.010
K22.7065.0246.635
9．已知不等式$\sqrt{x}+\sqrt{y}≤a\sqrt{x+y}$对一切x＞0，y＞0恒成立，则实数a的取值范围为[$\sqrt{2}$，+∞）．
6．已知点A（x，y）为函数y=$\frac{1}{x}$图象上在第一象限内的动点，若x3+y3≥a（x+y）2恒成立，则实数a的取值范围是（-∞，$\frac{1}{2}$]．
13．已知数列{an}是公差为d的等差数列，{bn}是公比为q（q∈R，q≠1，q≠0）的等比数列．若a1=（d-2）2，a3=d2，b1=（q-2）2，b3=q2．
（1）求数列{an}，{bn}的通项公式；
（2）设数列{cn}对任意自然数n均有$\frac{c_1}{b_1}+\frac{c_2}{{2{b_2}}}+\frac{c_3}{{3{b_3}}}+…+\frac{c_n}{{n{b_n}}}={a_{n+1}}$，求c1+c3+c5+…+c2n-1的值．
3．已知向量$\overrightarrow{m}$=（2cosωx，1），$\overrightarrow{n}$=（$\sqrt{3}$sinωx-cosωx，a），其中（x∈R，ω＞0），函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$的最小正周期为π，最大值为3．
（1）求ω和常数a的值；
（2）求当x∈[0，$\frac{π}{2}$]时，函数f（x）的值域．
10．已知点列如下：P1（1，1），P2（1，2），P3（2，1），P4（1，3），P5（2，2），P6（3，1），P7（1，4），P8（2，3），P9（3，2），P10（4，1），P11（1，5），P12（2，4），…，则P60的坐标为（5，7）．
7．在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系（单位长度相同）．已知曲线C的极坐标方程为ρ=4cosθ，直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcos\frac{π}{6}}\\{y=-\sqrt{3}+tsin\frac{π}{6}}\end{array}\right.$（t为参数）．若点P在曲线C上，且P到直线l的距离为1，则满足这样条件的点P的个数为（　　）
A．1B．2C．3D．4
8．如图，已知圆O上的弦AC=BD，过点C作圆O的切线与BA的延长线相交于点E
（1）求证：∠ACE=∠BCD；
（2）若BE=9，CD=1，求BC的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网