题目内容
9.设数列{an}的前n项之积为Pn=a1a2…an(n∈N*),若Pn=2${\;}^{\frac{n(n-1)}{2}}$,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{9}}$=( )| A. | $\frac{127}{64}$ | B. | $\frac{511}{256}$ | C. | $\frac{1023}{512}$ | D. | $\frac{511}{512}$ |
分析 由题意得到a1a2…an=2${\;}^{\frac{n(n-1)}{2}}$,求得首项,取n=n-1得到${a}_{1}{a}_{2}…{a}_{n-1}={2}^{\frac{(n-1)(n-2)}{2}}$(n≥2),作商求得数列通项公式,并得到数列∴{$\frac{1}{{a}_{n}}$}是以1为首项,以$\frac{1}{2}$为公比的等比数列,由此求得答案.
解答 解:由Pn=a1a2…an(n∈N*),Pn=2${\;}^{\frac{n(n-1)}{2}}$,得a1a2…an=2${\;}^{\frac{n(n-1)}{2}}$,
∴${a}_{1}={2}^{0}=1$,${a}_{1}{a}_{2}…{a}_{n-1}={2}^{\frac{(n-1)(n-2)}{2}}$(n≥2),
两式作商得:${a}_{n}={2}^{n-1}$(n≥2),
当n=1时上式成立,
∴${a}_{n}={2}^{n-1}$(n≥2),
则$\frac{1}{{a}_{n}}=\frac{1}{{2}^{n-1}}$,$\frac{1}{{a}_{n+1}}=\frac{1}{{2}^{n}}$,
由$\frac{\frac{1}{{a}_{n+1}}}{\frac{1}{{a}_{n}}}=\frac{1}{2}$,
∴{$\frac{1}{{a}_{n}}$}是以1为首项,以$\frac{1}{2}$为公比的等比数列,
∴$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{9}}$=$\frac{1×(1-\frac{1}{{2}^{9}})}{1-\frac{1}{2}}=\frac{511}{256}$.
故选:B.
点评 本题考查数列递推式,考查了等比关系的确定,考查了等比数列的前n项和,是中档题.

| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
| A. | $\frac{1}{4030}$ | B. | $\frac{1}{2015}$ | C. | $\frac{2}{2015}$ | D. | 0 |
| A. | (2kπ,2kπ+π)k∈Z | B. | (2kπ,2kπ+2π)k∈Z | C. | (kπ,kπ+$\frac{π}{2}$)k∈Z | D. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
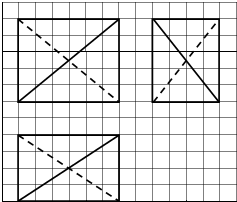 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )| A. | 40cm3 | B. | 50cm3 | C. | 60cm3 | D. | 80cm3 |
| A. | y=2-x | B. | y=tanx | C. | y=x3 | D. | y=log3x |