题目内容
19.如果复数$\frac{2-bi}{1+2i}$的实部和虚部互为相反数,则实数b=( )| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
分析 利用复数代数形式的乘除运算化简,由实部与虚部的和等于0求得b的值.
解答 解:由$\frac{2-bi}{1+2i}$=$\frac{(2-bi)(1-2i)}{(1+2i)(1-2i)}=\frac{(2-2b)-(b+4)i}{5}$=$\frac{2-2b}{5}-\frac{b+4}{5}i$,
又复数$\frac{2-bi}{1+2i}$的实部和虚部互为相反数,得2-2b-b-4=0,即b=-$\frac{2}{3}$.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
7.已知函数f(x)=e2x,g(x)=lnx+$\frac{1}{2}$,对?a∈R,?b∈(0,+∞),使得f(a)=g(b),则b-a的最小值为( )
| A. | $1+\frac{ln2}{2}$ | B. | $1-\frac{ln2}{2}$ | C. | $2\sqrt{e}-1$ | D. | $\sqrt{e}-1$ |
14.若a=$\frac{l{n}^{2}6}{4}$,b=ln2ln3,c=$\frac{l{n}^{2}2π}{4}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a<b<c | C. | c>a>b | D. | b>a>c |
9.设数列{an}的前n项之积为Pn=a1a2…an(n∈N*),若Pn=2${\;}^{\frac{n(n-1)}{2}}$,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{9}}$=( )
| A. | $\frac{127}{64}$ | B. | $\frac{511}{256}$ | C. | $\frac{1023}{512}$ | D. | $\frac{511}{512}$ |
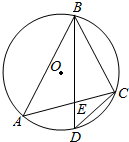 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.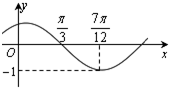 函数f(x)=Acos(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象.
函数f(x)=Acos(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数y=g(x)的图象.