题目内容
4.函数y=cos2(x+$\frac{π}{2}$)的单调递增区间( )| A. | (2kπ,2kπ+π)k∈Z | B. | (2kπ,2kπ+2π)k∈Z | C. | (kπ,kπ+$\frac{π}{2}$)k∈Z | D. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z |
分析 利用二倍角的余弦公式化简函数的解析式为y=$\frac{1}{2}-\frac{1}{2}cos2x$,令2kπ≤2x≤2kπ+π,k∈z,求得x的范围,可得函数的增区间.
解答 解:∵函数y=cos2(x+$\frac{π}{2}$)=sin2x=$\frac{1}{2}-\frac{1}{2}cos2x$,
∴令2kπ<2x<2kπ+π,k∈z,求得 kπ<x<kπ+$\frac{π}{2}$,可得函数的增区间为(kπ,kπ+$\frac{π}{2}$),k∈z,
故选:C.
点评 本题主要考查二倍角的余弦公式、余弦函数的增区间,属于基础题.

练习册系列答案
相关题目
14.若a=$\frac{l{n}^{2}6}{4}$,b=ln2ln3,c=$\frac{l{n}^{2}2π}{4}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a<b<c | C. | c>a>b | D. | b>a>c |
15.“a>b,c>0”是“ac>bc”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.设数列{an}的前n项之积为Pn=a1a2…an(n∈N*),若Pn=2${\;}^{\frac{n(n-1)}{2}}$,则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{9}}$=( )
| A. | $\frac{127}{64}$ | B. | $\frac{511}{256}$ | C. | $\frac{1023}{512}$ | D. | $\frac{511}{512}$ |
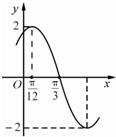 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.