题目内容
1．已知复数z=3+i（i为虚数单位），则z的共轭复数$\overline z$在复平面内对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用共轭复数的概念即得结论．
解答 解：∵z=3+i，∴$\overline{z}$=3-i，
∴$\overline z$在复平面内对应的点为（3，-1），
故选：D．
点评 本题考查复数的几何意义，注意解题方法的积累，属于基础题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
9．设数列{an}的前n项之积为Pn=a1a2…an（n∈N*），若Pn=2${\;}^{\frac{n（n-1）}{2}}$，则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{9}}$=（ ）
| A． | $\frac{127}{64}$ | B． | $\frac{511}{256}$ | C． | $\frac{1023}{512}$ | D． | $\frac{511}{512}$ |
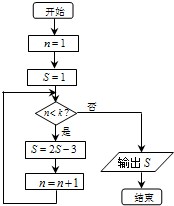
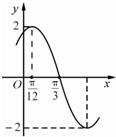如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）图象的一部分．
如图所示，四棱锥P-ABCD的底面ABCD是直角梯形，BC∥AD，AB⊥AD，AB=BC=$\frac{1}{2}$AD，PA⊥底面ABCD，过BC的平面交PD于M，交PA于N（M与D不重合）．