题目内容
5.函数f(x)=log2(4-x2)的定义域为(-2,2),值域为(-∞,2],不等式f(x)>1的解集为$({-\sqrt{2},\sqrt{2}})$.分析 先利用对数的真数大于0求该函数的定义域,根据函数图象来求其值域;根据题意列出不等式,通过解不等式求f(x)>1的解集.
解答 解:依题意得:4-x2>0,
解得-2<x<2,
所以该函数的定义域为:(-2,2).
∵4-x2>0,
∴(4-x2)最大值=4,
∴在(-2,2)上,该函数的值域为:(-∞,2].
由f(x)>1得到:log2(4-x2)>1,
则4-x2>2,
解得-$\sqrt{2}$<x<$\sqrt{2}$.
故不等式f(x)>1的解集为 $({-\sqrt{2},\sqrt{2}})$.
故答案是:(-2,2);(-∞,2];$({-\sqrt{2},\sqrt{2}})$.
点评 本题考查了对数函数定义域的求法,考查了对数函数的值域,是基础的计算题.

练习册系列答案
相关题目
20.观察下列各式:

照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )

照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )
| A. | 4n+1 | B. | 4n | C. | 4n-1 | D. | 4n-2 |
10.设$\overrightarrow a$是非零向量,λ为负实数,下列结论中正确的是( )
| A. | $\overrightarrow a$与$λ\overrightarrow a$的方向相反 | B. | $|{λ\overrightarrow a}|≥|{\overrightarrow a}|$ | ||
| C. | $\overrightarrow a$与${λ^2}\overrightarrow a$的方向相同 | D. | $|{λ\overrightarrow a}|=|λ|\overrightarrow a$ |
17.已知圆x2+y2=4,直线l:y=x+b,圆上至少有三个点到直线l的距离都是1,则b的取值范围是( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | {-$\sqrt{2}$,$\sqrt{2}$} | C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | [0,$\sqrt{2}$] |
14.已知数列{an}的前n项和Sn=n2-2n,则 a2+a10=( )
| A. | 20 | B. | 19 | C. | 18 | D. | 17 |
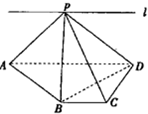 如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.