题目内容
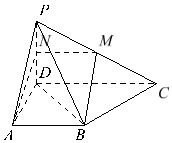
【题目】如图,已知四棱锥的侧棱![]() 底面
底面![]() ,且底面
,且底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在侧棱上.
在侧棱上.
(1)求证:![]() 平面
平面![]() ;
;
(2)若侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

【答案】(1)见解析;(2) ![]() .
.
【解析】
试题分析:(1)要证明![]() 平面
平面![]() ,就是要证
,就是要证![]() 与平面
与平面![]() 内两条相交直线垂直,由已知
内两条相交直线垂直,由已知![]() 底面
底面![]() ,得
,得![]() ,因此还要证
,因此还要证![]() (们是相交的直线),这个可利用勾股定理可得;(2)由已知得棱
(们是相交的直线),这个可利用勾股定理可得;(2)由已知得棱![]() 与底面
与底面![]() 所成角就是
所成角就是![]() ,即
,即![]() ,要求异面直线
,要求异面直线![]() 和
和![]() 所成的角,我们一般平移其中一条直线使之与另一条相交,图中由于
所成的角,我们一般平移其中一条直线使之与另一条相交,图中由于![]() ,
,![]() 为
为![]() 的中点,取
的中点,取![]() 的中点
的中点![]() ,则有
,则有![]() 且
且![]() ,从而
,从而![]() 且
且![]() ,因此
,因此![]() 是平行四边形,
是平行四边形,![]() ,则
,则![]() 就是异面直线
就是异面直线![]() 和
和![]() 所成的角,解三角形可得.
所成的角,解三角形可得.
试题解析:(1)由已知可算得![]() ,
,![]()
![]() ,
,
故![]() ,
,
 又
又![]() ,
,![]() 平面
平面![]() ,故
,故![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ;………………………6分
;………………………6分
(2)如图,取PD中点为N,并连结AN,MN,易证明![]() ,
,
则![]() 即异面直线
即异面直线![]() 与
与![]() 所成角;
所成角;
又![]() 底面
底面![]() ,
,![]() 即为
即为![]() 与底面
与底面![]() 所成角,
所成角,
即![]() ,
,![]()
![]() ,即
,即![]() ,
,
易求得![]() ,
,![]() ,则在
,则在![]() 中,
中,![]() ,
,
即异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() . ………………………12分
. ………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目